Détection d'anomalie
01 May 2020
Data Challenge Airbus sur la détection d'anomalie
Les données
Les données d’Airbus contiennent des mesures d’accéléromètre d’hélicoptère. Chaque observation correspond à une minute d’enregistrement à 1024 Hertz donnant des séries temporelles de $60 * 1024 = 61440$ points équidistants.
- Entrainement: 1677 observations
- Test: 2511 observations
Le critère de performance
Le critère de performance à optimiser est l’aire sous la courbe ROC (AUC). Cette mesure est fréquement utilisée lorsque les classes sont déséquilibrées. Ceci est typiquement le cas en détection d’anomalies où les observations anormales sont beaucoup plus rares que les observations normales.
- Interprétation de L’AUC:
L’AUC correspond à la probabilité d’affecter un score plus élevé à un échantillon positif par rapport à un négatif en ayant tiré aléatoirement les deux échantillons dans chacune des classes.
Table des matière
- Introduction
- 1. Exploraition des données
- 2. Classification dans le domaine temporel
- 3. Classification dans le domaine fréquentiel
- 4. Approche mixte temporelle et fréquentielle
- 5. Approche en Deep Learning
- Conculsion
Introduction
La difficulté majeure de la detection d’anomalie fonctionnelle est de trouver la représentation des données permettant de décrire le mieux possible le comportement normal du système. Le choix de la transformation peut être facilité par la connaissance à priori des sources d’anomalies. Dans le cas de la detection d’anomalie des roulements à bille par exemple, la déterioration des roulements va entrainer l’apparition de fréquences vibratoires absentes dans le cas d’un comportement normal.
Deux méthodes sont proposées pour detecter les anomalies:
- Une consiste à chercher les descripteurs les plus appropriés pour detecter les anomalies (feature engineering) puis d’appliquer des algorithmes de detection d’anomalie non supervisés comme l’algorihtme d’Isolation Forest ou bien Local Outlier Factor.
- L’autre utilise des méthodes de Deep Learning pour apprendre la représentation des données en utilisant des autoencodeurs ou en cherchant un sous espace de volume minimum des données.
Cadre de detection d’anomalie
Le jeu d’entrainement ne comporte pas d’observation anormale, nous somme donc dans le cadre de ce qui est parfois appelé la detection d’anomalie semi-supervisée. Il est possible d’apprendre le comportement normal du système avec le jeu d’entrainement et d’utiliser les scores d’anomalies de plusieurs algorithmes non supervisés pour prédire la probabilité qu’une observation soit anormale.
1. Exploration des données
1.1 Statistiques sur les séries temporelles
Dans un premier temps, nous pouvons nous intéresser au caractéristiques statistiques du signal dans le domaine temporel en regardant la distribution de la moyenne, variance, coefficient d’asymétrie, kurtosis…


On remarque que la distribution de la moyenne est plus étendue pour le jeu d’entrainement que pour le jeu de test, signifiant potentiellement que des observations anormales du jeu de test pourraient être détectées en utilisant la moyenne des observations.
Description statistique de données en normalisant toutes les courbes
On peut regarder les mêmes statistiques en normalisant chaques courbes par leurs valeurs maximales.


La destributions des statistiques des courbes normalisées ressemblent à celles calculées précédemment.
1.2 Analyse dans le domaine fréquentiel
La transformée de Fourier est une représentation naturelle des signaux stationnaires, c’est à dire dont le contenu informationnel ne varie pas au cours du temps. C’est un outils couramment utilisé en traitment du signal puiqu’elle permet d’extraire les fréquences composant un signal et d’appliquer facilement des filtres. Dans notre cas, cet outils est intéressant puisqu’il peut réduire le dimension des signaux composés de quelques fréquences majoritaires. On peut espérer que ces fréquences captent l’information sur les anomalies des signaux.
Les signaux tracés correspondent aux 5 signaux classés comme les plus normaux par le classifieur précédent en ayant réduit les séries à leurs moyennes et diffénces temporelles maximale. On remarque que les signaux ont des pics de fréquences à 26 et 53 Hz. Ces fréquences peuvent être relié à une excitation vibratoire provenant d’un arbre tournant à $26*60 = 1560 \ tr/min $. On remarque que les signaux classifiés comme anormaux ont une puissance spectrale plus importante en basse fréquence venant du fait que les signaux sont classifié selon leurs moyenne et qu’un signal ayant une moyenne plus élevé à une plus grande puissance spectrale en basse fréquence.
Le désaventage de la transformé de Fourier est sa résolution nulle dans le domaine temporel. Dans le cadre de la détection d’anomalie, des phénomènes transitoires ou des ruptures brutales sont fréquemment observés, et il devient légitime de considérer plutôt une description des signaux à la fois en temps et en fréquence comme la transformée de Fourier à court terme 5.2 ou la transformé en ondelette 5.4.
2. Classification dans le domaine temporel
2.1 Moyenne seule
Note sur le score donné par l’algorithme Isolation Forest:
- Les prédictions de l’algorithme correspondent à la profondeur moyenne d’une observation sur l’ensemble des arbres construits. Moins la profondeur est grande plus l’observation est anormale puisqu’elle est en moyenne isolée rapidement dans la construction de l’arbre.
- Dans le cadre du challenge, il est demandé de donner un score plus important aux observations les plus anormales. Il faudra donc penser à prendre l’opposé du résultat lors des soumissions.
Remarque:
L’échelle des scores donnés par sklearn est translatée de telle sorte à ce que les scores négatif correspondent à des anomalies. La translation est calculée par rapport aux taux de contamination à priori (0.1 par défaut).
X_test = np.mean(xtest, axis = 1)[:, None]
model = IsolationForest(n_estimators=3000)
model.fit(X_test)
score = model.decision_function(X_test)
- Score: 0.7123
En utilisant comme seul descrpiteur des séries temporelles la moyenne, en choisissant aléatoirement une observation normale et une anormale, notre classifieur prédit le bon label (anomalie ou non) avec probabilité 71,2%
On peut se demander s’il est possible d’améliorer la prédiction en utilisant des moments statisques dans la prédiction comme le Kurtosis ou le coefficient d’asymétrie
2.2 Moyenne, coefficient d’asymétrie, Kurtosis
def build_features(data):
features = {}
for k in range(3, 5):
features["moment_" + str(k)] = stats.moment(data, moment=k, axis=1)
features["mean"] = np.mean(data, axis=1)
return pd.DataFrame(features)
X_train = build_features(xtrain)
X_test = build_features(xtest)
model = IsolationForest(n_estimators=3000)
model.fit(X_train)
score = model.decision_function(X_test)
- Score: 0.637
Ajouter d’autre descripteur simple de la série temporelle diminue l’AUC. Cela signifie que des observations normale on des kurtosis et coefficients d’asymétries élévés. Cet exemple montre la difficulté de la détection d’anomalie. Les descripteurs doivent permettre d’isoler les anomalies.
2.3 Moyenne et différence première
def build_features(data):
features = {}
features["max_first_diff"] = np.max(np.abs(data[:, 1:] - data[:, :-1]), axis=1)
features["mean"] = np.mean(data, axis=1)
return pd.DataFrame(features)
X_train = build_features(xtrain)
X_test = build_features(xtestc_clean)
model = IsolationForest(n_estimators=5000)
model.fit(X_test)
score = model.decision_function(X_test)
_ = construct_predictions(-score)
- score: 0.727
La différences premières des des séries temporelle permet d’améliorer la classification des anomalies
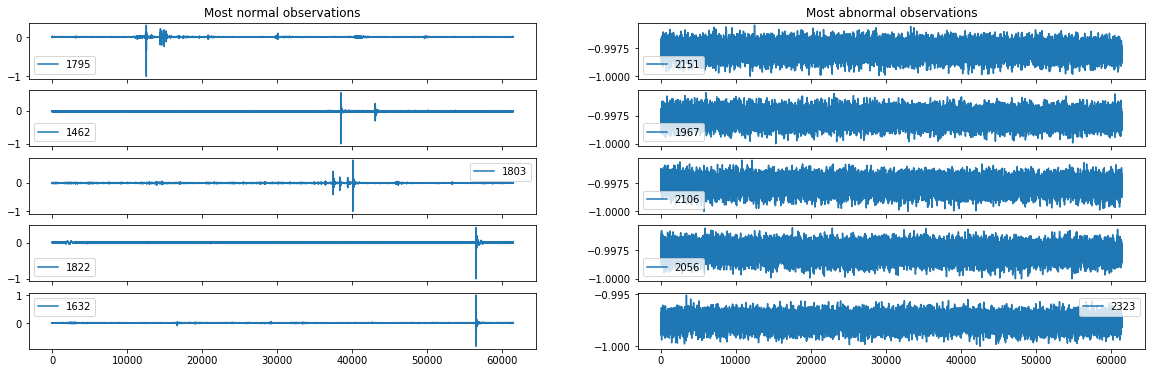
Tracé des observations les plus normales et les plus anormales
- Il est intéressant de regarder les observations classifiées comme les plus anormales et les plus normales par notre classifeur afin de comprendre les origines des anomalies. On souhaite connaitre la structure globale des courbes normales ainsi que celle anormales.
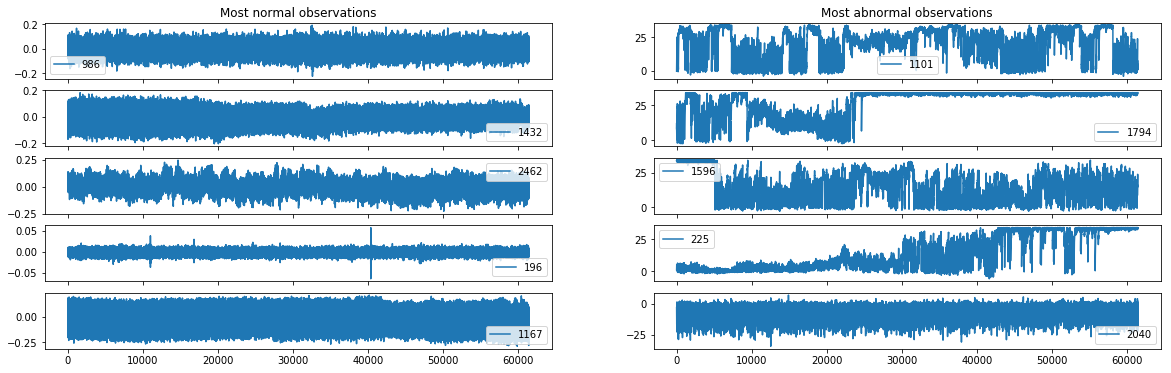
On constate que les courbes classifiées comme normale sont beaucoup moins ératiques que les courbes anormales et qu’elles sont aussi plus stables par rapport à leurs moyennes. Ceci est bien sur du au fait que les anomalies sont classifiées sur la base de la moyenne et de la différence première. C’est seulement le score obtenu lors du test qui permet de juger si ces descripteurs sont bons ou mauvais pour prédire les anomalies.
3. Classification dans le domaine fréquentiel
3.1 En utilisant la densité spectrale des signaux
L’idée ici est classifier les anomalies en utilisant la densité spectrale de puissance des signaux. Les descrpiteurs retenus sont les k pics de la puissance spectrale avec ses fréquences associées.
- Exemple de recherche de pics dans un périodogramme pour deux observations
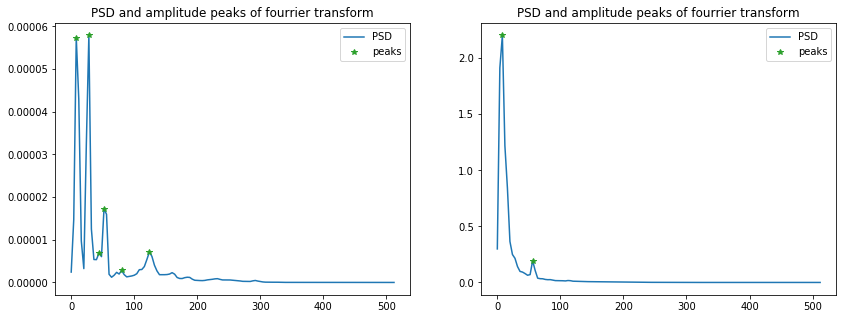
- Construction des descripteurs pour k=5
def construct_features(data, nfreq=5):
features_matrix = np.empty((len(data), nfreq*2))
for k in tqdm(range(len(data))):
freq, psd = signal.welch(data[k, :], fs=1024)
peaks, _ = signal.find_peaks(psd)
ind_max_psd = np.argsort(psd[peaks])[-(nfreq+1):-1]
psd_max = psd[ind_max_psd]
freq_max = freq[ind_max_psd]
features_matrix[k, :] = np.hstack((psd_max, freq_max))
return features_matrix
xtrain_ = construct_features(xtrain)
xtest_ = construct_features(xtest_clean)
X_train_ = pd.concat([X_test, pd.DataFrame(xtest_)], axis=1)
model = IsolationForest(n_estimators=2000)
model.fit(X_train_)
sscore = model.decision_function(X_train_)
construct_predictions(sscore)
- Score: 0.629
Le score montre que le description fréquentielle n’est pas suffisante pour classifier de façon précise les anomalies. Une approche mixte est donc proposée dans la section suivante.
4. Approche mixte temporelle et frequentielle
4.1 Descripteurs fréquentiels et temporels
Les observations d’origines sont projetés ici dans un espace à 3 dimensions contenant:
- la moyenne des signaux
- le maximum des différences premières
- la fréquence correspondant à la puissance spectrale a plus importante
def transform_positif_features(feature):
sorted_feature = np.sort(feature)
new_feature = np.zeros((score.shape))
ind = np.argsort(feature)
sorted_feature = sorted_feature * (-1)**np.arange(len(sorted_feature))
new_feature[ind] = sorted_feature
return new_feature
def build_features(data):
features = {}
features["max_first_diff"] = np.max(np.abs(data[:, 1:] - data[:, :-1]), axis=1)
features["mean"] = np.mean(data, axis=1)
features["median"] = np.median(data, axis=1)
features["skew"] = stats.skew(data, axis=1)
return pd.DataFrame(features)
X_test = build_features(xtestc_clean)
X_test['most_imp_freq'] = freqs
model = IsolationForest(n_estimators=10000)
model.fit(X_test)
score = model.decision_function(X_test)

- score : 0.735
La prise en compte de la fréquence correspondant à la puissance spectrale a plus importante améliore la prédiction.
Utilisation d’autres descripteurs
- En prennant les 2 premières fréquences:
- score: 0.739
- En ajoutant la médiane
- score: 0.771
- En ajoutant la médiane et le coefficient d’assymétrie
- score: 0.793
Le meilleur resultat (AUC = 0.793) lors de ce challenge a été obtenu en appliquant l’algorithme d’isolation Forest sur les données projetées sur:
- La moyenne
- La médiane
- La différence première maximale
- La fréquence correspondant à la puissance spectrale a plus importante
- Le coefficient d’asymétrie (skew)
4.2 Stacking
Les prédictions de plusieurs algorithme de détection d’anomalie peuvent être utilisés pour améliorer la robustesse des prédictions. La librairies pyod propose une implémentation simple d’aggrégation de modèle. Le score final peut être le score maximal des différents modèles, la moyenne ou la médiane.
Cette façon de procéder demande un réglage précis des hyperparamêtres de chaque modèle (nombre de voisin pour LOF, nombre de clusters pour CBLOF…). L’algorithme Isolation Forest à l’avantage d’avoir peut d’hyperparamêtres à régler (nombre d’arbres construits , nombre de variables tirées aléatoirement pour chaque partition).
La stacking de modèle n’a pas permis ici d’améliorer le modèle, à cause du réglage peu fin des hyperparamêtres.
from pyod.models.ocsvm import OCSVM
from pyod.models.lof import LOF
from pyod.models.cblof import CBLOF
from pyod.models.iforest import IForest
from pyod.models.mcd import MCD
from pyod.models.lscp import LSCP
from pyod.models.combination import maximization, average
model = LSCP([IForest(n_estimators=5000), LOF(), CBLOF(), OCSVM(), MCD()], n_bins=2)
models = [IForest(n_estimators=5000), LOF(), CBLOF(), OCSVM(), MCD()]
scores = np.empty((X_test.shape[0], len(models)))
for k, model in tqdm(enumerate((models))):
model.fit(X_test)
scores[:, k] = model.decision_function(X_test)
5. Approche en deep Learning
Le désavantage des méthodes précédemment utilisées sont l’extraction des descripteurs des données manuelle, demandant beaucoup de connaissances à priori sur la génération des anomalies.
Le but d’une approche en Deep Learning est d’apprendre la représentation des données adéquates pour détecter les anomalies par des réseaux de neuronnes. La plupart des méthodes développées ces dernières années conciste à construire un autoencodeur et d’utiliser l’erreur de reconstruction comme détection d’anomalie. La difficulté du choix des descripteurs des données devient celle du choix de l’architecture du réseau de neurone notamment le degré de compression des données (le nombre de neurones intermédiaires de l’autoencodeur).
Cette méthode est utilisée en 5.1 et 5.2 en apprenant un autoencodeur convolutionnel sur respectivement les séries temporelles brutes et sur les transformées de Fourier à court terme.
Une deuxième méthode Deep One-Class Classification, 2019 conciste à trouver l’ensemble de volume minimal des données en entrainant un réseau de neurone minimisant le volume de l’hypersphère inscrite aux données. Cette formulation force le réseau de neurone à extraire les facteurs commun de variation. Le problème de minimisation ressemble à la formulation des SVM et dans le cas du noyau Gaussien, les deux méthodes convergent asymptotiquement.
5.1 A partir des séries temporelles
Architecture utilisée
L’architecture est constituée de:
- 4 convolutions 1D de taille 4 et max pooling de taille 2
- 2 couches fully connected
- 4 convolutions 1D de taille 4 et d’up sampling de taille 2
Autoencoder avec convolution 1D
n_filters1 = 10
n_filters2 = 10
n_filters3 = 10
n_filters4 = 10
dropout=0.01
model = tf.keras.models.Sequential([
tf.keras.layers.Conv1D(filters=n_filters1, kernel_size=4, padding="same", input_shape=(61440, 1), strides=2, activation=tf.nn.relu),
tf.keras.layers.MaxPool1D(pool_size=2, strides=None, padding='same'),
tf.keras.layers.Dropout(dropout),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Conv1D(filters=n_filters2, kernel_size=4, padding="same", strides=2, activation=tf.nn.relu),
tf.keras.layers.MaxPool1D(pool_size=2, strides=None, padding='same'),
tf.keras.layers.Dropout(dropout),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Conv1D(filters=n_filters3, kernel_size=4, padding="same", strides=2, activation=tf.nn.relu),
tf.keras.layers.MaxPool1D(pool_size=2, strides=None, padding='same'),
tf.keras.layers.Dropout(dropout),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Conv1D(filters=1, kernel_size=4, padding="same", strides=2, activation=tf.nn.relu),
tf.keras.layers.MaxPool1D(pool_size=2, strides=None, padding='same'),
tf.keras.layers.Dropout(dropout),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Reshape((240,)),
tf.keras.layers.Dense(20),
# --- bottleneck --- #
tf.keras.layers.Dense(240),
tf.keras.layers.Reshape((240, 1)),
tf.keras.layers.UpSampling1D(size=2),
Conv1DTranspose(filters=n_filters4, kernel_size=4, padding="same", strides=2),
tf.keras.layers.Dropout(dropout),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.UpSampling1D(size=2),
Conv1DTranspose(filters=n_filters3, kernel_size=4, padding="same", strides=2),
tf.keras.layers.Dropout(dropout),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.UpSampling1D(size=2),
Conv1DTranspose(filters=n_filters2, kernel_size=4, padding="same", strides=2),
tf.keras.layers.Dropout(dropout),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.UpSampling1D(size=2),
Conv1DTranspose(filters=n_filters1, kernel_size=4, padding="same", strides=2),
tf.keras.layers.Dropout(dropout),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Conv1D(filters=1, kernel_size=1, padding="same", strides=1),
])
print(model.summary())
- Entrainement du modèle
if os.path.exists("NN-models/time-srie-AE.h5"):
print("loading model")
model = tf.keras.models.load_model("NN-models/time-serie-AE.h5")
else:
model.compile(optimizer='adam',
loss=tf.losses.MSE)
logdir = "logs/time-serie-AE/" + datetime.now().strftime("%Y%m%d-%H%M%S")
tensorboard_callback = tf.keras.callbacks.TensorBoard(log_dir=logdir, histogram_freq = True)
with tf.device('/GPU:0'):
model.fit(xtrainc[:, :, None], xtrainc[:, :, None], epochs=100, batch_size=64, shuffle=True, verbose=1)
model.save('NN-models/time-serie-AE.h5')
xtrain_pred = model.predict(xtrainc[:, :, np.newaxis])
reconstr = model.predict(xtestc_clean[:, :, np.newaxis])
reconstr = reconstr[:, :, 0]
- Utilisation de l’erreur de reconstruction pour prédire les anomalies
score = np.mean((xtestc_clean - reconstr)**2, axis=1)
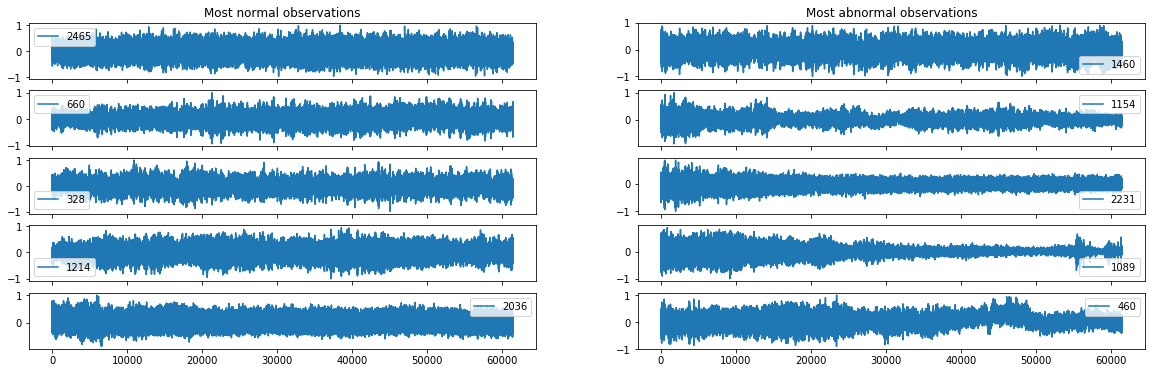
- Visualisation des observations les plus normales et anormales
plot_minmax_scores(score, xtestc_clean)
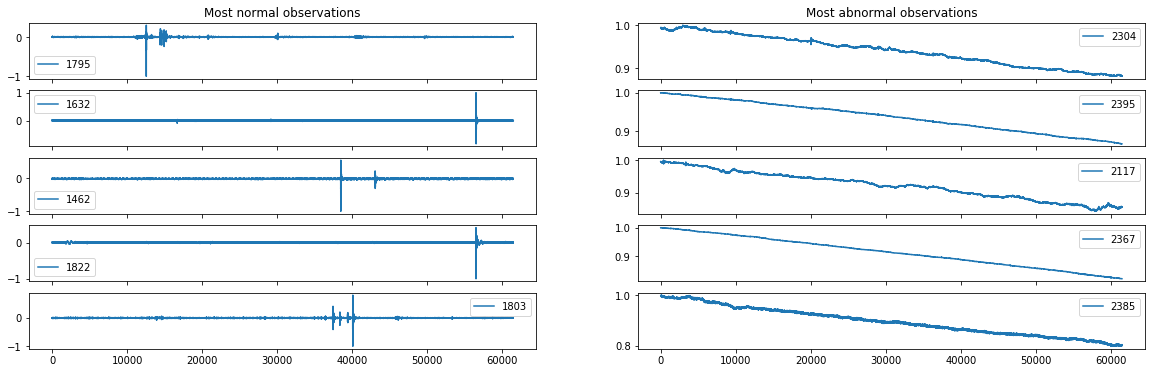
- Score: 0.621
L’architechture proposée ici ne permet pas de bien déterminer les anomalies. L’approche Deep Learning est très intéressante et satisfaisante d’un point de vue théorique comparé au feature engineering mais est assez difficile à mettre en oeuvre.
5.2 A partir de la transformée de Fourier à court terme
Utilisation de la transformée de Fourier à court terme pour apprendre le comportement normal.
- Transformation des séries temporelles dans le domaine {temps, fréquence}
- Utilisation d’un autoencodeur convolutionnel
- Utilisation de l’erreur de reconstruction comme detection d’anomalie
Exemple de transformée à court terme de certaines observations
_, ax = plt.subplots(2, 5, figsize=(20, 10), sharex='col', sharey='row')
indices_clean = [1039, 1167, 528, 1432, 2461, 1101, 1794, 1596, 225, 2040]
# --- train data --- #
for k, ind in enumerate(indices_clean[:5]):
f, t, Zxx = signal.stft(xtest_clean[ind, :], fs=1024, nperseg=500)
ax[0][k].pcolormesh(t, f, np.abs(Zxx), cmap='RdBu_r')
ax[0][k].set_title('STFT Magnitude train ' + str(ind))
ax[0][k].set_ylabel('Frequency [Hz]')
ax[0][k].set_xlabel('Time [sec]')
# --- test data --- #
for k, ind in enumerate(indices_clean[5:]):
f, t, Zxx = signal.stft(xtest_clean[ind, :], fs=1024, nperseg=500)
ax[1][k].pcolormesh(t, f, np.abs(Zxx), cmap='RdBu_r')
ax[1][k].set_title('STFT Magnitude test ' + str(ind))
ax[1][k].set_ylabel('Frequency [Hz]')
ax[1][k].set_xlabel('Time [sec]')
plt.show()
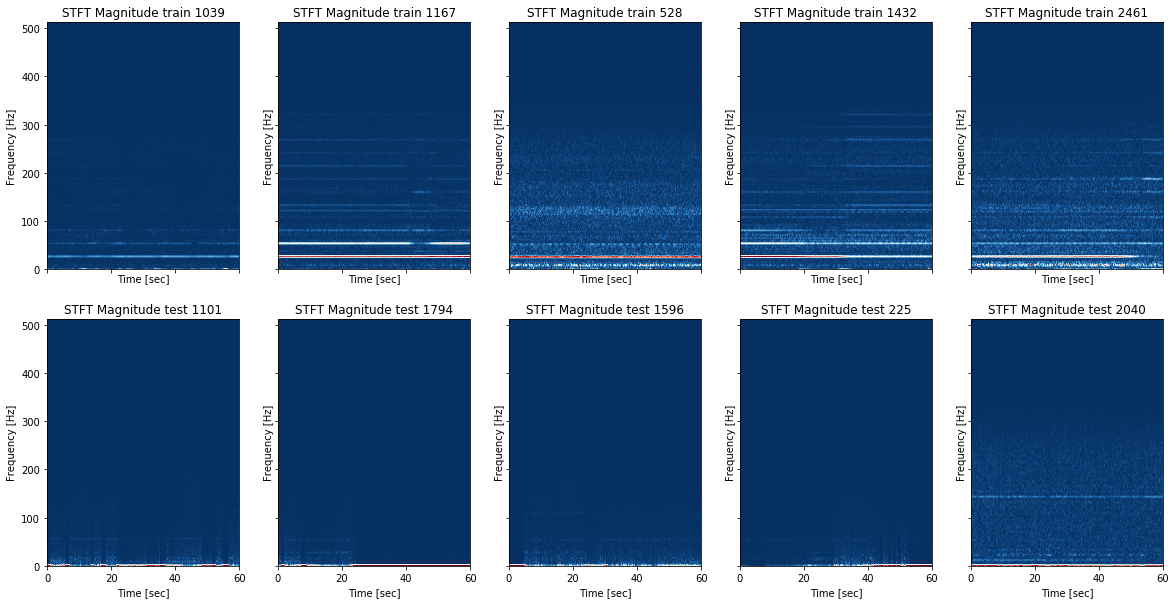
- Construction des données transformées
encoding_dim = 2048
input_shape = Zxx.shape
encoder_net = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(input_shape[0], input_shape[1], 1)),
tf.keras.layers.Conv2D(4, 4, strides=2, padding='same', activation=tf.nn.relu),
tf.keras.layers.Conv2D(8, 4, strides=2, padding='same', activation=tf.nn.relu),
tf.keras.layers.Conv2D(16, 4, strides=2, padding='same', activation=tf.nn.relu),
tf.keras.layers.Conv2D(32, 4, strides=2, padding='same', activation=tf.nn.relu)
])
decoder_net = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(16, 16, 32)),
tf.keras.layers.Conv2DTranspose(32, 4, strides=2, padding='same', activation=tf.nn.relu),
tf.keras.layers.Conv2DTranspose(16, 4, strides=2, padding='same', activation=tf.nn.relu),
tf.keras.layers.Conv2DTranspose(8, 4, strides=2, padding='same', activation=tf.nn.relu),
tf.keras.layers.Conv2DTranspose(4, 4, strides=2, padding='same', activation='sigmoid'),
tf.keras.layers.Conv2D(1, (6,10), strides=1, padding='valid', activation='sigmoid')
])
print(encoder_net.summary())
print(decoder_net.summary())
X_train, X_valid = train_test_split(xtrain_, test_size=0.05, random_state=42)
X_train = X_train[:, :, :, None]
X_valid = X_valid[:, :, :, None]
model = tf.keras.models.load_model("NN-models/AE-WFFT.h5")
if os.path.exists("NN-models/AE-WFFT.h5"):
print("loading model")
model = tf.keras.models.load_model("NN-models/AE-WFFT.h5")
else:
model = tf.keras.Sequential([encoder_net, decoder_net])
model.compile(optimizer='adam',
loss=tf.losses.MSE)
logdir = "logs/scalars/" + datetime.now().strftime("%Y%m%d")
tensorboard_callback = tf.keras.callbacks.TensorBoard(log_dir=logdir, histogram_freq = True)
model.fit(X_train, X_train, epochs=20, batch_size=64,
callbacks=[tensorboard_callback, PeriodicLogger()], shuffle=True, validation_data=(X_valid, X_valid), verbose=0)
model.save("NN-models/AE-WFFT.h5")
reconstr = model.predict(xtest_[:, :, :, None])
- Calcul de l’erreur de reconstruction
reshape_xtest = xtest_.reshape(xtest_.shape[0], xtest_.shape[1]*xtest_.shape[2])
reshape_reconstr = reconstr[:, :, :, 0].reshape(xtest_.shape[0], xtest_.shape[1]*xtest_.shape[2])
score = np.mean((reshape_xtest - reshape_reconstr)**2, axis=1)
- Quelques reconstructions de transformée de Fourier à court terme par l’autoencodeur
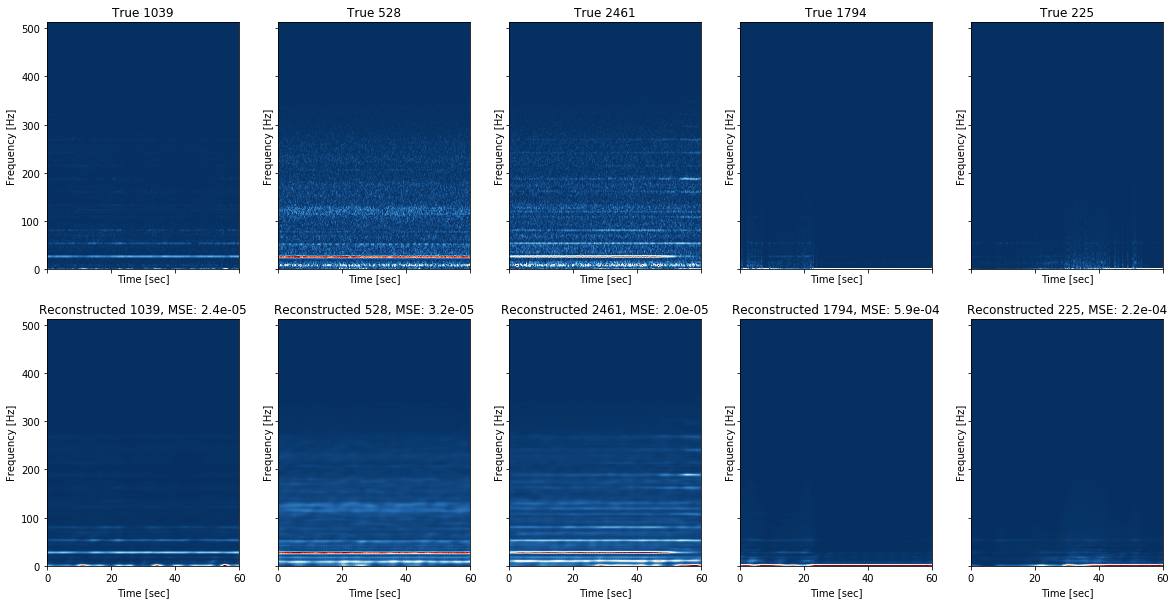
L’autoencodeur arrive à bien reconstruire les spectrogrammes en retirant notamment le bruit.
- Visualisation des observations les plus normales et anormales
- Score: 0.621
On remarque que certains signaux prédit comme anormaux par les algorithmes vus précédemment sont très bien reconstruits par l’autoencodeur. Ceci s’explique par l’architecture utilisée de convolution qui rend le modèle invariant par translation. Nous avons vu que certaines observations anormales provenaient d’un décallage de la moyenne, augmentant ainsi la puissance en basse fréquence. Ces signaux ne peuvent pas être détecter par le modèle établis à cause de l’invariance par translation des convolutions.
5.3 Recherche de la projection de volume minimum
Implementation PyTorch de Deep SVDD
sys.path.append("./deepsvdd/src")
from deepsvdd.src.networks import windowed_FFT_SVDD, mnist_LeNet
from deepsvdd.src.deepSVDD import DeepSVDD
from deepsvdd.src.base.base_dataset import BaseADDataset
import torch
from sklearn.model_selection import train_test_split
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
class ADDataset(BaseADDataset):
def __init__(self, train, test):
super().__init__()
self.train = train
self.test = test
def loaders(self, batch_size: int, shuffle_train=True, shuffle_test=False, num_workers: int = 0):
train = torch.utils.data.DataLoader(self.train, batch_size=batch_size, shuffle=shuffle_train)
test = torch.utils.data.DataLoader(self.test, batch_size=batch_size, shuffle=False)
return train, test
dsvdd = DeepSVDD()
dsvdd.set_network('sensor_time_series')
data = ADDataset(torch.tensor(xtrainc[:, None, :], device=device).float(),
torch.tensor(xtestc_clean[:, None, :], device=device).float())
net = dsvdd.train(data, n_epochs=1000)
net = dsvdd.train(data, n_epochs=100)
dsvdd = DeepSVDD()
dsvdd.set_network('sensor_time_series')
data = ADDataset(torch.tensor(xtrain_[:, None, :, :], device=device).float(),
torch.tensor(xtest_[:, None, :, :], device=device).float())
net = dsvdd.train(data, n_epochs=50)
score = dsvdd.test(data)
5.4 Autres recherches
Utilisation de la transformée en ondelette
La transformée en ondelette à l’avantage d’avoir une résolution temporelle qui s’adapte en fonction de la fréquence. La transformée de Fourier à court terme à une résolution temporelle constante en fonction de la fréquence ce qui rend impossible par exemple de repérer simultanément un son de basse et un coup de caisse claire dans un enregistrement de musique. La transformée en ondelette à une résolution temporelle qui augmente avec la fréquence rendant possible cette distinction dans un spectrogramme. La résolution fréquentielle décroit alors aussi avec la fréquence (inégalité d’Heisenberg).
Transformée en ondelette de certaines observations
La transformée en ondelette est tracée pour les 5 signaux classés commes les plus normaux (en haut) par les modèles de la partie précédente et les plus anormaux (en bas).
fig, ax = plt.subplots(2, 5, figsize=(20, 5), sharey=True, sharex=True)
time = np.arange(xtrain.shape[1])
indices_clean = [1039, 1167, 528, 1432, 2461, 1101, 1794, 1596, 225, 2040]
for i, ind in tqdm(enumerate(indices_clean), position=0):
signal_ = xtestc_clean[ind, :]
scales = np.arange(1, 200)
freq = 1024
dt = 1 / freq
coefs, freq = pywt.cwt(signal_, scales, wavelet='morl', sampling_period=dt, method='fft')
im = plot_wavelet(time, coefs, freq, levels_increment=1.7, ax=ax[i//5][i%5])
ax[i//5][i%5].set_title("xtest " + str(ind))
plt.suptitle("Wavelet Transform (Power Spectrum) of signal", fontsize=18)
plt.show()
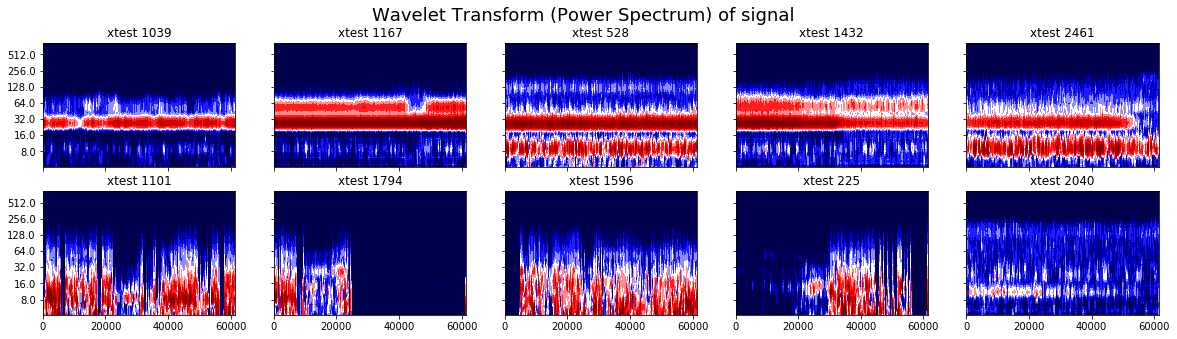
La transformée en ondelette semble plus prometteuse à distinguer les observations normales et anormales. L’approche n’a pas été poursuivie à cause de la taille conséquente des spectrogrammes obtenus mais serait intéressante à mettre en oeuvre.
Conclusion
Le challenge proposé montre les subtilités de la detections d’anomalies dans un cadre non supervisé. Contrairement au cadre supervisé, il est difficile de juger la qualité du modèle pendant son élaboration. Le tracé des observations classées comme les plus normales et anormales par l’algorithme peut donner tout de même une indication sur le type d’anomalies détectées par le modèle.
Nous avons vu que les méthodes classiques de machine learning permettent d’obtenir de bon résultat même si l’approche Deep Learning est plus satisfaisante. Cette dernière mérite d’être approfondie en cherchant des architectures permettant de mieux représenter les données. Beaucoup de méthodes n’ont pas été développées, comme une approche utilisant de LSTM où bien l’utilisation de GAN.
