Économétrie
15 April 2020
Séries temporelles et autocorrélation des résidus
Cette page présente un projet d’économétrie réalisé pendant mon année à Télécom Paris. Le but est d’analyser la relation entre le taux de chômage et le taux d’inflation (voir courbe de Phillips). Cette relation est étudiée à travers les séries temporelles de l’indice d’inflation (CPI) et du taux de chômage. Dans le cadre des régressions sur des séries temporelle, il est fréquent que les résidus soit autocorrélés. Le modèle à tendance à se tromper plus à l’instant $t$ s’il s’est trompé à l’instant $t-1$. Des techniques de sphériscisation des résidus sont proposés en modélisant le processus des bruits par un modèle AR(p).
Stationnariser la série de CPI en utilisant la méthode de régression qui inclue un terme de tendance dont la forme fonctionnelle est à choisir
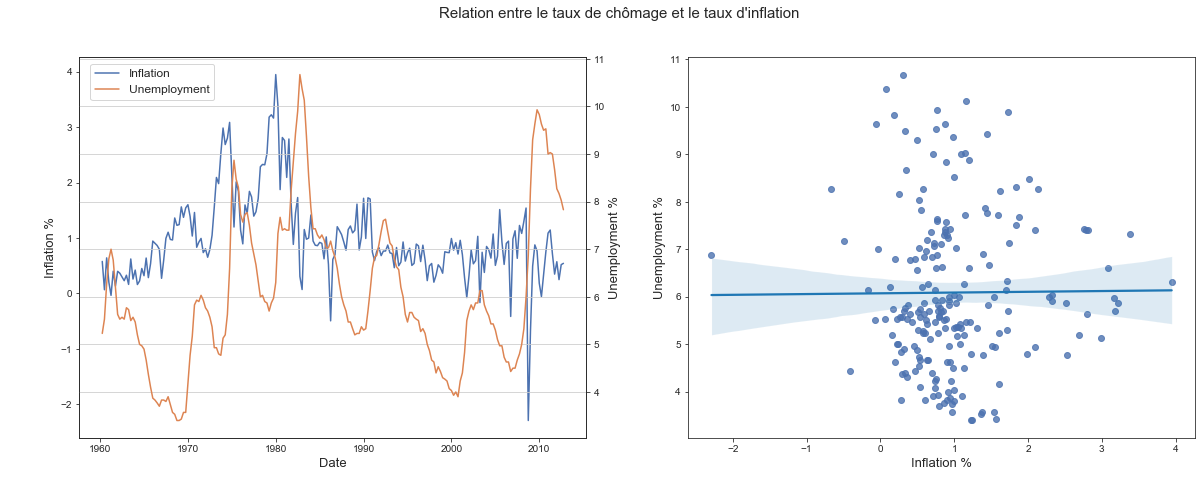
Tracé du l’indice d’inflation depuis 1960:
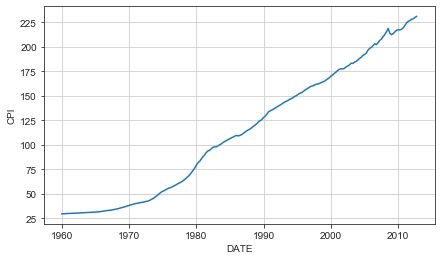
Le CPI correspond à l’indice des prix qui augmente lorsque qu’il y a de l’inflation. Les banques centrale ont un objectif d’inflation de 2% ce qui explique pourquoi cette courbe est croissante dans l’ensemble.
Plusieurs options sont possibles pour stationnariser la série temporelle:
- Utiliser les différences premières de la série ce qui donnerait le série temporelle du taux d’inflation $\bf r$
- Faire une regression du terme de tendance
- Ici le tendance à deux modes, un plutot exponentielle en début de courbe puisque pour un taux d’inflation constant par exemple, le CPI peut s’écrire: $CPI = \theta_0 \ r^t$
- Un deuxième mode plutot linéaire
Nous allons donc tester trois tendances:
-
Linéaire
-
Exponentielle
-
Hyperbolique
Et regarder la stationnarité des résidus pour chaque modèlsation.
def hyperbole(x, a0, a, b, alpha):
return a0 + (b + a*x**alpha)**(1/alpha)
# --- modèle de tendance linéaire --- #
X = sm.add_constant(quarterly.index)
y = quarterly.CPI
model = sm.OLS(y, X)
results = model.fit()
y_hat_linear = results.predict(X)
res_linear = quarterly.CPI - y_hat_linear
# --- modèle de tendance exponentielle --- #
y = np.log(quarterly.CPI)
model = sm.OLS(y, X)
results = model.fit()
y_hat_exp = np.exp(results.predict(X))
res_exp = quarterly.CPI - y_hat_exp
# --- modèle hyperbolique --- #
t = quarterly.index.values
y = quarterly.CPI
xmin = [-100, 0, 0, 0.1]
xmax = [100, 1e7, 1e7, 10]
loss = lambda x: np.mean((y - hyperbole(t, *x)) ** 2)
x0 = [30, 0.01, 0.1, 4]
bounds = [(low, high) for low, high in zip(xmin, xmax)]
ret = basinhopping(loss, x0, minimizer_kwargs={"method":"L-BFGS-B", "bounds":bounds}, niter=200)
y_hat_hyp = hyperbole(t, *ret.x)
res_hyp = quarterly.CPI - y_hat_hyp
- Tracé des différentes tendances
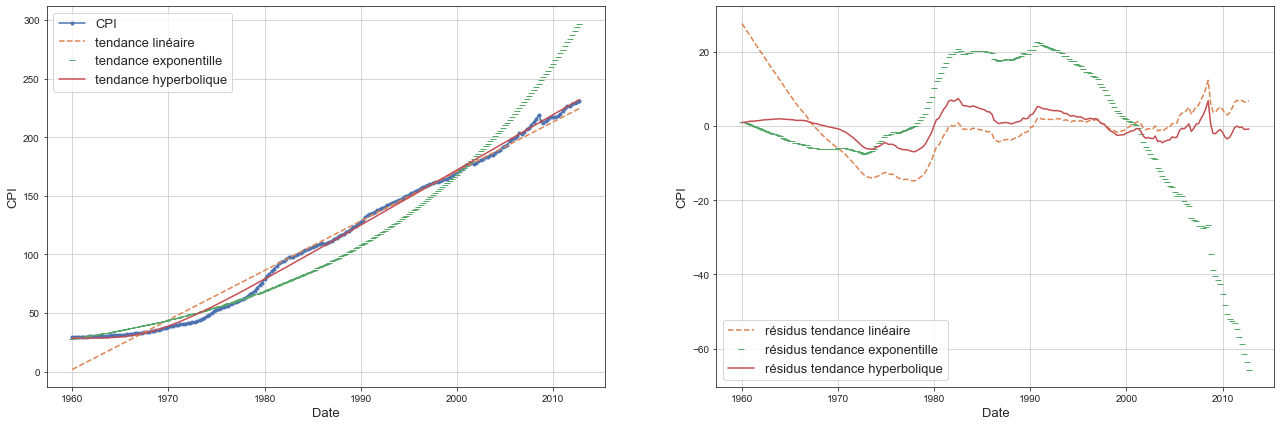
- On voit que la meilleure forme fonctionnelle pour expliquer la tendance est hyperbolique.
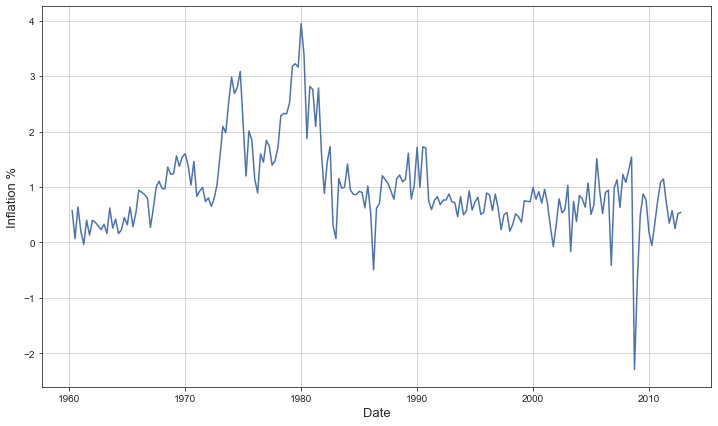
2. Calculer inf, le taux d’inflation à partir de la variable CPI
_, ax = plt.subplots(figsize=(12, 7))
inflation = (quarterly["CPI"] - quarterly["CPI"].shift(1)) / quarterly["CPI"].shift(1) * 100 # set inf in %
inflation = inflation.dropna()
inflation.name = "inf"
ax.plot(quarterly.DATE[1:], inflation, label="Inflation", color=COLORS[0])
ax.set_xlabel('Date', fontsize=13)
ax.set_ylabel('Inflation %', fontsize=13)
plt.grid()
plt.show()
Interpréter l’autocorrélogramme et l’autocorrélogrammes partiels de inf. Quelle est ladifférence entre ces deux graphiques ?
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(20, 7))
plot_acf(inflation.dropna(), ax=ax1)
plot_pacf(inflation.dropna(), ax=ax2)
plt.show()
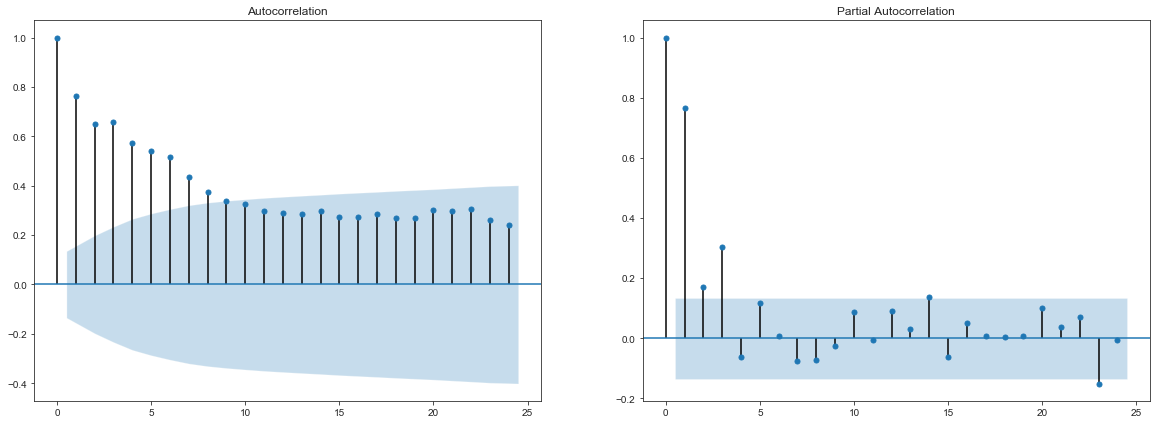
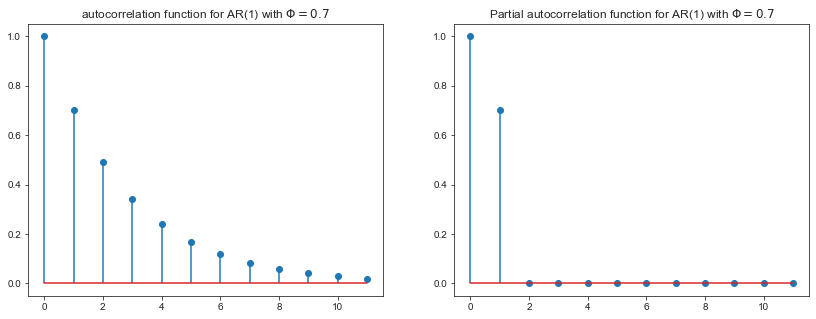
- L’autocorrélogramme correspond au calcul des corrélations des valeurs de la série temporelle avec sa version décallée d’ordre $s$. $\rho(s) = \frac{cov(X_tX_{t-s})}{var(X_t)}$.
- L’autocorrélation partielle représente la corrélation entre $X_t$ et les résidus de la regression de $X_t$ sur ses versions décallées d’ordre $[1..s]$ connu sous le nom de processus d’innovation.
Ces fonctions font parties des représentations fondamentales des séries temporelles (avec la représentation spectrale et celle de Wold) dans le sens deux séries sont égales ssi leurs fonctions d’autocorrélations sont égales.
Ces deux réprésentations sont particulièrement pratiques pour détecter l’ordre des processus $AR(p)$ ou $MA(q)$.
- Un processus $MA(q)$ à:
- Ses p premiers coefficient d’autocorrélation non nuls, et tous les autres nuls.
- Ses p premiers coefficents d’autocorrélation partielle quelconque et une décroissance de composition de sinus et d’exponentielles pour les suivants.
- Un processus $AR(p)$ à un comportement symétrique.
phi = 0.7
leg = np.arange(12)
rho = phi**leg
partial_rho = np.hstack(([1, phi], np.zeros(10)))
_, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))
ax1.stem(leg, rho, use_line_collection=True)
ax1.set_title(f"autocorrelation function for AR(1) with $\\Phi={phi}$")
ax1.set_label("lags")
ax2.stem(leg, partial_rho, use_line_collection=True)
ax2.set_title(f"Partial autocorrelation function for AR(1) with $\\Phi={phi}$")
ax2.set_label("lags")
plt.show()
Quelle est la différence entre la stationnarité et l’ergodicité ? Pourquoi a-t-on besoin de ces deux conditions. Expliquez le terme “spurious regression”.
- Une série temporelle est fortement stationnaire si la loi de distribution jointe de ${ x_{t-s}, .., x_t, .., x_{t+s} }$ ne dépend pas du temps. On définit aussi la stationnarité faible lorsque les moments d’ordre 1 et 2 d’une série temporelle ne dépendent pas du temps.
La stationnarité est indispensable pour faire de l’estimation précise des paramètres d’un processus. Ceci est par exemple connu pour les régressions falacieuses qui montre des relations entres des processus non stationnaire qui n’ont pas de sens. Par exemple, dans le cas de la regression de deux processus AR(1) avec racine unitaire, la distribution classique de l’estimateur des coefficients n’est plus selon une loi de Student, mais selon un mouvement brownien.
- Un processus ergodique est un processus stochastique pour lequel les statistiques peuvent être approchées par l’étude d’une seule réalisation suffisamment longue. Un processus non ergodique change de façon ératique à un rythme inconsistant.
L’ergodiscité est une hypothèse fondamentale pour l’étude des séries temporelles puisque les processus ne sont connus qu’à travers une de leurs réalisation. Il est alors possible de faire des estimations de paramètres (moyenne, variance…).
- Exemple de régression falacieuse
Avec $\epsilon_t \ et \ \mu_t \sim \mathcal{N}(0, 1)$
x_0 = np.random.standard_normal()
y_0 = np.random.standard_normal()
x = [x_0]
y = [y_0]
for k in range(1000):
x.append(x[k] + np.random.standard_normal())
y.append(y[k] + np.random.standard_normal())
model = sm.OLS(y, sm.add_constant(x))
results = model.fit()
display_html(OLS_summary(results))
| parameters | cov | HC3 | p_values | |
|---|---|---|---|---|
| const | -14.3924 | 0.2516 | 0.2761 | 0.000 |
| x_1 | -0.1028 | 0.0192 | 0.0179 | 0.000 |
- On remarque en appliquant les statistiques de test usuelles que la variable x de la régression est significative alors que par construction x et y sont indépendant.
Faire le test Augmented Dickey Fuller pour inf en utilisant utilisant le critère AIC pour déterminer le nombre de lags à inclure.
df_stat = adfuller(inflation.dropna(), autolag='AIC')
pd.DataFrame({"adfuller-stat": df_stat[0], "p-value": df_stat[1], "n-lags": df_stat[2], "n_points_used": df_stat[3],
"1%": df_stat[4]["1%"], "5%":df_stat[4]["5%"], "10%": df_stat[4]["10%"], "max_inf_criterion": df_stat[5]}, index=["values"])
| adfuller-stat | p-value | n-lags | n_points_used | 1% | 5% | 10% | max_inf_criterion | |
|---|---|---|---|---|---|---|---|---|
| values | -2.919056 | 0.043177 | 2 | 208 | -3.462186 | -2.875538 | -2.574231 | 276.758307 |
L’hypothèse nulle de racine unitaire n’est pas rejetée à 5%. L’inflation est certainement un processus DF (differency stationnary).
Proposer une modélisation AR(p) de inf
Les tracés d’autocorrélation et d’autocorrélation partielle de l’inflation ressemble à ceux d’un processus $AR(1)$ ou $AR(3)$.
- On peut aussi utiliser les critères d’information AIC et BIC pour estimer le meilleur ordre du modèle $AR$
AIC = []
BIC = []
for lag in range(1, 20):
ar_model = AutoReg(inflation.dropna().values, lags=lag).fit()
AIC.append(ar_model.aic)
BIC.append(ar_model.bic)
plt.figure(figsize=(12, 7))
plt.plot(range(1, 20), AIC, label="AIC")
plt.plot(range(1, 20), BIC, label='BIC')
plt.legend()
plt.show()
print(f"lag optimal selon le critère BIC: {np.argmin(BIC) + 1}")
print(f"lag optimal selon le critère AIC: {np.argmin(AIC) + 1}")
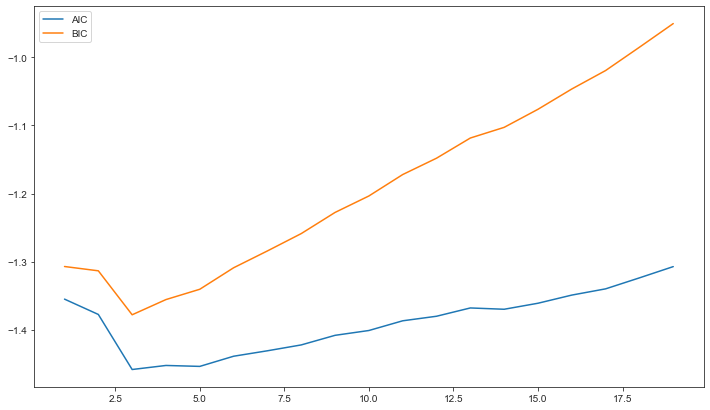
Les critères AIC et BIC sont minimaux pour un nombre de lag=3 .
Un modèle $AR(3)$ semble être la meilleure modèlisation de l’inflation
Explication du taux de chômage en fonction du taux d'inflation
Estimer le modèle de la courbe de Philips qui explique le taux de chômage (Unemp) en fonction du taux d’inflation courant et une constante.
- Tracé du taux de chômage en fonction de l’inflation
- Regression linéaire
X = sm.add_constant(inflation)
y = quarterly.Unemp[1:]
model = sm.OLS(y, X)
results = model.fit()
residual = results.resid
display_html(OLS_summary(results))
| parameters | cov | HC3 | p_values | |
|---|---|---|---|---|
| const | 6.0708 | 0.1808 | 0.1724 | 0.000 |
| inf | 0.0159 | 0.1444 | 0.1164 | 0.912 |
Sans vérifications des conditions d’optimalités de l’estimateur OLS, on ne peut pas conclure sur l’influence du taux de chomage sur l’inflation. Cependant, même si le coeffcient de la regression se retrouve à être significatif avec des méthodes d’estimation des MCG, cette influence sera faible.
- hétérocsédasticité
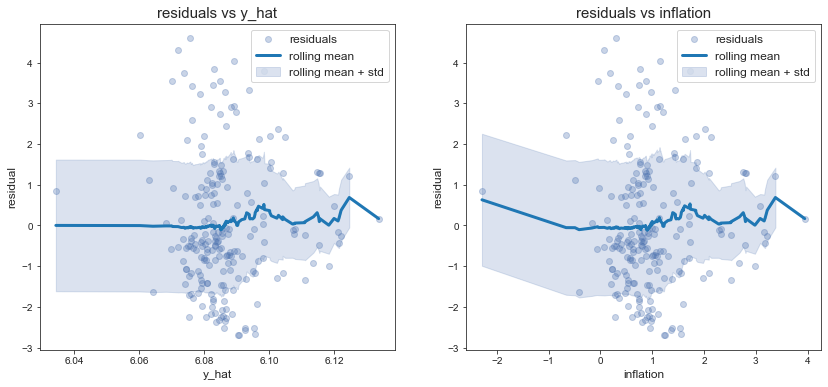
Les résidus semblent hétéroscédastique en regardant la moyenne mobile en fonction de l’inflation
Tester l’autocorrélation des erreurs
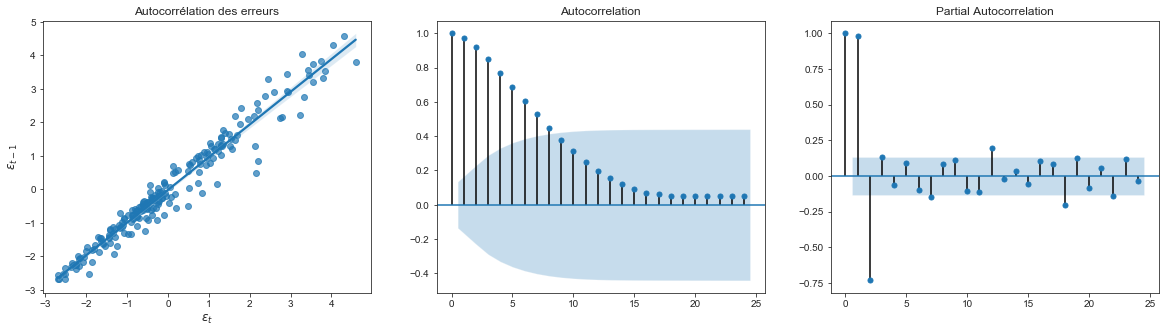
- On remarque une forte autocorrélation des erreurs du modèle. Ceci est frèquent dans l’étude des séries temporelles. Le modèle à tendance à se tromper plus à l’instant $t$ s’il s’est trompé à l’instant $t-1$.
Nous allons appliquer le test de Durbin-Watson pour tester l’autocorrélation des erreurs à l’ordre 1.
Le modèle considéré est:
\[\epsilon_t = \rho \epsilon_{t-1} + u_t\]Et on teste l’hypothèse nulle:
\[H_0 = \{ \rho = 0 \}\]La statistique de test est:
\[d = \frac{\sum_{t=2}^{T}(\epsilon_t - \epsilon_{t-1})^2}{\sum_{t=1}^{T}\epsilon_t^2} \rightarrow 2(1 - \hat{\rho})\]d = np.sum((residual - residual.shift(1))**2) / np.sum(residual**2)
rho = 1 - d/2
print("Durbin-Watson coefficient: {:.3f}".format(d))
print("rho: {:.3f}".format(rho))
Durbin-Watson coefficient: 0.044
rho: 0.978
-
La loi asymptotique de cette estimateur n’est pas connue analytiquement mais il existe des tables permettant de tester la significativité du test.
-
Les résidus sont autocorrélés
-
Le test d’autocorrélation des résidus peut être réalisé par MCO sur les résidus estimés. Le test de significativité par MCO est valable seulement asymptotiquement. Les deux estimations convergent vers la même valeurs.
model = sm.OLS(residual[1:], residual.shift(1)[1:])
results = model.fit()
display_html(OLS_summary(results))
| parameters | cov | HC3 | p_values | |
|---|---|---|---|---|
| rho | 0.9799 | 0.0145 | 0.0156 | 0.000 |
On obtient la même estimation de $\rho$ avec une estimation par moindres carrés.
Corriger l’autocorrélation des erreurs par la méthode vue en cours
D’après le graphe de l’autocorrélation partielle, on remarque que les résidus suivent un modèle $AR(2)$. Nous allons donc procéder à l’estimation des paramêtres $AR$ et ensuite soit appliquer les MCG en calculant la matrice d’autocorrélation des résidus, soit en appliquant sphéricisant les variables avant d’appliquer les MCO.
- Calcul des paramètres $AR(2)$
phi, sigma = sm.regression.yule_walker(residual, order=2, method="mle")
pd.DataFrame({"Phi1": phi[0], "Phi2": phi[1]}, index=["paramètres"])
| Phi1 | Phi2 | |
|---|---|---|
| paramètres | 1.554159 | -0.594903 |
- Calcul de la matrice de covariance avec les relations de yule_walker
Et en utilisant la récursion $\rho_k = \Phi_1 \rho_{k-1} + \Phi_2 \rho{k-2}$ pour calculer les autres.
Ces valeurs peuvent être calulées en utilisant les résultats des suites récurrentes linéaires d’ordre 2.
\[\Delta = \Phi_1^2 + 4\Phi_2\]Si $\Delta > 0$: \(\rho_k = \lambda r_1^k + \mu r_2^k \ \text{avec} \ (r_1, r_2) \ \text{les racines du polynome} \ X^2 - \Phi_1 X - \Phi_2\)
\[r_{1-2} = \frac{\Phi_1 \pm \sqrt{\Phi_1^2 + 4\Phi_2}}{2}\]Et:
\[\left\{ \begin{array}{ccccc} \rho_0 &=& \lambda &+& \mu \\ \rho_1 &=& \lambda r_1 &+& \mu r_2 \\ \end{array} \right.\]Ce qui donne:
\[\left\{ \begin{array}{cc} \mu &= \frac{\rho_1 - r_1}{r_2-r_1} \\ \lambda &= 1 - \mu \\ \end{array} \right.\]# -- roots of the caractéristic equation of the serie -- #
delta = phi[0]**2 + 4*phi[1]
r1 = (phi[0] + np.sqrt(delta))/2
r2 = (phi[0] - np.sqrt(delta))/2
# -- Yule-Walker equation to compute rho1 and rho2 --
rho1 = phi[0] / (1 - phi[1])
rho2 = phi[0]*rho1 + phi[1]
# -- initial conditions of the serie -- #
mu = (rho1 - r1) / (r2 - r1)
lambda_ = 1 - mu
# -- compute all autocorrelation value -- #
n = residual.shape[0]
rho = lambda_ * r1 ** np.arange(n) + mu * r2 ** np.arange(n)
- Comparaison de l’autocorrélation obtenue avec un processus $AR(2)$ et l’autocovariance estimée des résidus
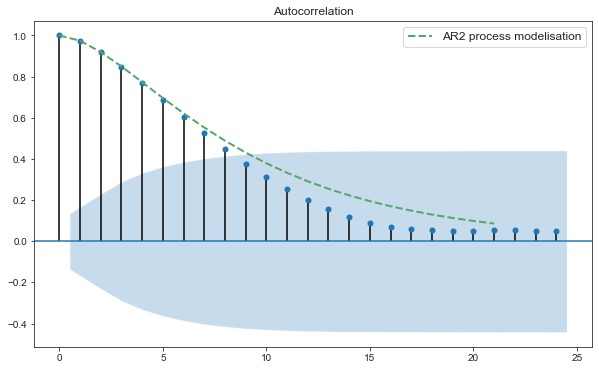
def build_sigma(n, rho):
"""
build covariance matrix of AR(p) process from the
autocorrelation sequence rho
"""
rho = rho[:n]
sigma = np.empty((n, n))
for k in range(n):
sigma[k, :] = np.roll(rho, k)
return sigma
- Nous pouvons aussi appliquer la méthode des moindres carrés génréralisés en spécifiant la matrice de covariance des erreurs:
X = sm.add_constant(quarterly.Unemp)[1:]
y = inflation
n, p = X.shape
sigma = build_sigma(n, rho)
model = sm.GLS(y, X, sigma=sigma)
results = model.fit()
display_html(OLS_summary(results))
| parameters | cov | HC3 | p_values | |
|---|---|---|---|---|
| const | 0.9654 | 0.2080 | 0.1582 | 0.000 |
| Unemp | 0.0037 | 0.0330 | 0.0266 | 0.911 |
Tester la stabilité de la relation chômage-inflation sur deux sous-périodes de taille identique.
X = sm.add_constant(inflation)
y = quarterly.Unemp[1:]
n, p = X.shape
ind = n // 2
sigma = build_sigma(n, rho)
model = sm.GLS(y, X, sigma=sigma)
results = model.fit()
SSE_c = np.sum(results.resid**2)
# -- regression for the first division -- #
X1 = X[:ind]
y1 = y[:ind]
results = sm.OLS(y1, X1).fit()
residual = results.resid
sigma = build_sigma(ind, rho)
model = sm.GLS(y1, X1, sigma=sigma)
results = model.fit()
SSE1 = np.sum(results.resid**2)
# -- regression for the second division -- #
X2 = X[ind:]
y2 = y[ind:]
results = sm.OLS(y1, X1).fit()
residual = results.resid
sigma = build_sigma(n - ind, rho)
model = sm.GLS(y2, X2, sigma=sigma)
results = model.fit()
SSE2 = np.sum(results.resid**2)
f_stat = ((SSE_c-(SSE1+SSE2)) / p) / ((SSE1+SSE2)/(n-2*p))
p_value = f.sf(f_stat, p, n-2*p)
display_html(pd.DataFrame({"f-stat": f_stat, "p-value": p_value}, index=["results"])\
.style.format({'f-stat': "{:.3f}", 'p-value': "{:.3f}"}))
| f-stat | p-value | |
|---|---|---|
| results | 1.933 | 0.147 |
Le test de changement de strucute est significatif. On accepte donc l’hypothèse de changement de structure entre les deux sous groupes.
Faites les tests changement de structure de Chow et détecter le point de rupture
def regression_over_period(ind: int, use_sigma=True):
X1 = X[:ind]
y1 = y[:ind]
sigma = build_sigma(ind, rho)
if use_sigma:
model = sm.GLS(y1, X1, sigma=sigma)
else:
model = sm.GLS(y1, X1)
results = model.fit()
SSE1 = np.sum(results.resid**2)
# -- regression for the second division -- #
X2 = X[ind:]
y2 = y[ind:]
sigma = build_sigma(n - ind, rho)
if use_sigma:
model = sm.GLS(y2, X2, sigma=sigma)
else:
model = sm.GLS(y2, X2)
results = model.fit()
SSE2 = np.sum(results.resid**2)
return SSE1, SSE2
plt.figure(figsize=(12, 7))
fisher = []
for ind in range(20, 150):
SSE1, SSE2 = regression_over_period(ind, use_sigma=use_sigma)
fisher.append( ((SSE_c-(SSE1+SSE2)) / p) / ((SSE1+SSE2)/(n-p)))
plt.plot(quarterly.DATE[20:150], fisher)
plt.title("Test de Chow pour différent valeur t de changement de structure")
plt.xlabel("periode de changement de structure")
plt.ylabel("test de Fisher")
plt.grid()
plt.show()
print(f"Changement de structure le plus significatif: {quarterly.DATE[np.argmax(fisher)+20]}")
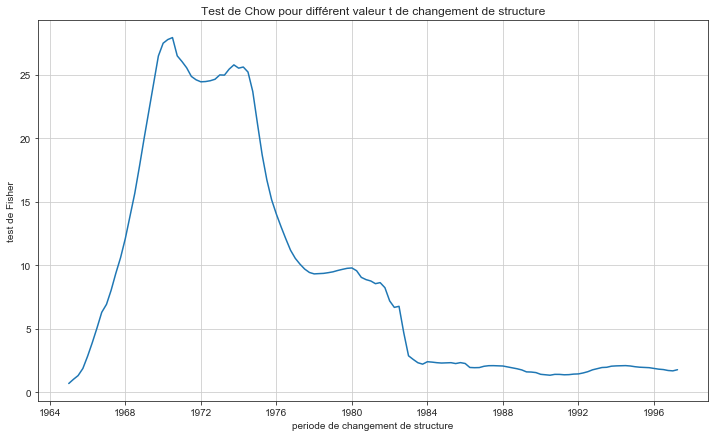
- Ce changement de structure correspond à 3ème trimestre de 1970.
Estimer la courbe de Philips en supprimant l’inflation courante des variables explicatives mais en ajoutant les délais d’ordre 1, 2, 3 et 4 de l’inflation et du chômage. Faire le test de Granger de non causalité de l’inflation sur le chômage.
X = pd.concat([pd.concat([inflation.shift(i) for i in range(1, 5)], axis=1), pd.concat([quarterly.Unemp.shift(i) for i in range(1, 5)], axis=1)], axis=1)
new_names = []
for i, name in enumerate(X.columns):
new_names.append(name + '_' + str((i%4+1)))
X.columns = new_names
X = X[5:]
X = sm.add_constant(X)
X.head(2)
| const | inf_1 | inf_2 | inf_3 | inf_4 | Unemp_1 | Unemp_2 | Unemp_3 | Unemp_4 | |
|---|---|---|---|---|---|---|---|---|---|
| 5 | 1.0 | 0.201478 | 0.642109 | 0.067636 | 0.578231 | 6.8 | 6.27 | 5.53 | 5.23 |
| 6 | 1.0 | -0.033512 | 0.201478 | 0.642109 | 0.067636 | 7.0 | 6.80 | 6.27 | 5.53 |
- Test de causalité de Granger
Nous allons appliquer le test de Fisher de nullité des coefficient associés à $inf$ dans la régression de:
\[inf_t = \beta_0 + \beta_{inf_1}inf_{t-1}+ \beta_{inf_2}inf_{t-2}+ \beta_{inf_3}inf_{t-3}+ \beta_{inf_4}inf_{t-4} + \beta_{Unemp_1}Unemp_{t-1}+ \beta_{Unemp_2}Unemp_{t-2}+ \beta_{Unemp_3}Unemp_{t-3}+ \beta_{Unemp_4}Unemp_{t-4}\]# --- regression with all variables --- #
y = quarterly.Unemp[5:]
n, p = X.shape
model = sm.OLS(y, X)
results = model.fit()
residual = results.resid
SSE = np.sum(residual**2)
# --- regression without Unemp variable (beta_Unemp_i = 0 in the f-test) --- #
X1 = sm.add_constant(X.iloc[:, 5:])
y = quarterly.Unemp[5:]
model = sm.OLS(y, X1)
results1 = model.fit()
residual1 = results1.resid
SSE1 = np.sum(residual1**2)
# --- Compute Fisher Stat --- #
f_stat = ((SSE1 - SSE) / 4) / (SSE / (n - 4))
p_value = f.sf(f_stat, 4, n - 4)
results_fisher = pd.DataFrame({"f-stat": f_stat, "p-value": p_value}, index=["results"])\
.style.format({'f-stat': "{:.3f}", 'p-value': "{:.3f}"})
display_html(results_fisher)
display_html(OLS_summary(results))
| f-stat | p-value | |
|---|---|---|
| results | 3.893 | 0.005 |
| parameters | cov | HC3 | p_values | |
|---|---|---|---|---|
| const | 0.1457 | 0.0724 | 0.0859 | 0.045 |
| inf_1 | 0.0311 | 0.0376 | 0.1224 | 0.409 |
| inf_2 | -0.0236 | 0.0409 | 0.0870 | 0.565 |
| inf_3 | 0.0689 | 0.0399 | 0.0387 | 0.085 |
| inf_4 | 0.0163 | 0.0376 | 0.0565 | 0.664 |
| Unemp_1 | 1.5937 | 0.0712 | 0.1132 | 0.000 |
| Unemp_2 | -0.6472 | 0.1339 | 0.2260 | 0.000 |
| Unemp_3 | 0.0222 | 0.1354 | 0.1932 | 0.870 |
| Unemp_4 | -0.0080 | 0.0702 | 0.0833 | 0.910 |
- La p-valeur du test de fisher est 0.005, on rejette l’hypothèse nulle de non significativité globale des coefficient. On peut ainsi dire au sens de Granger qu’il y a une relation de causalité du chômage sur l’inflation.
Représentez graphiquement les délais distribués et commentez. Calculer l’impact à long terme de l’inflation sur le chômage
fig, ax = plt.subplots(1, 2, figsize=(16, 5))
ax[0].stem(range(1, 5), results.params[1:5], use_line_collection=True)
ax[0].set_title("Coefficients associés à l'inflation en fonction du délais dans la regression", fontsize=12)
ax[0].set_xlabel("Délais inflation", fontsize=12)
ax[0].set_xticks(range(1, 5))
ax[1].stem(range(1, 5), results.params[5:], use_line_collection=True)
ax[1].set_title("Coefficients associés au taux de chomage en fonction du délais dans la regression", fontsize=12)
ax[1].set_xlabel("Délais chomage", fontsize=12)
ax[1].set_xticks(range(1, 5))
plt.show()
print("Somme des coefficients associés à l'inflation: {0:0.3f}".format(np.sum(results.params[1:5])))
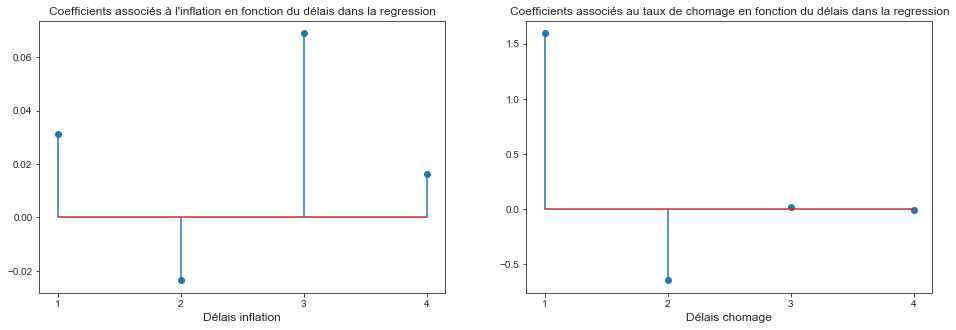
Somme des coefficients associés à l'inflation: 0.093
-
Les délais coefficient de la regression associé aux délais distribués de l’inflation suivent la même tendance son l’autocorrélogramme. Ceux associés au taux de chômage suivent la tendance d’un modèle AR à coefficients négatif.
-
Sur le long terme, si on considère que le taux de chomage est stable sur 3 trimestres, puisque $\sum_{i=1}^{4} \theta_{Unemp-i} = 0.093$ on peut dire que sur le long terme, le taux d’intérêt n’a pas d’influence sur le taux de chômage. Une hausse de 1 point de l’inflation entraîne une hausse de 0.093 point du taux de chomage. C’est la vision monétariste de la courbe de Phillips.
Explication du taux d'inflation en fonction du taux de chômage
Afin de suivre l’ordre usuel des variables de la courbe de Phillips, l’étude est aussi réalisée en prennant comme variable éxogène le taux de chômage.
- Tracé du taux de chômage en fonction de l’inflation
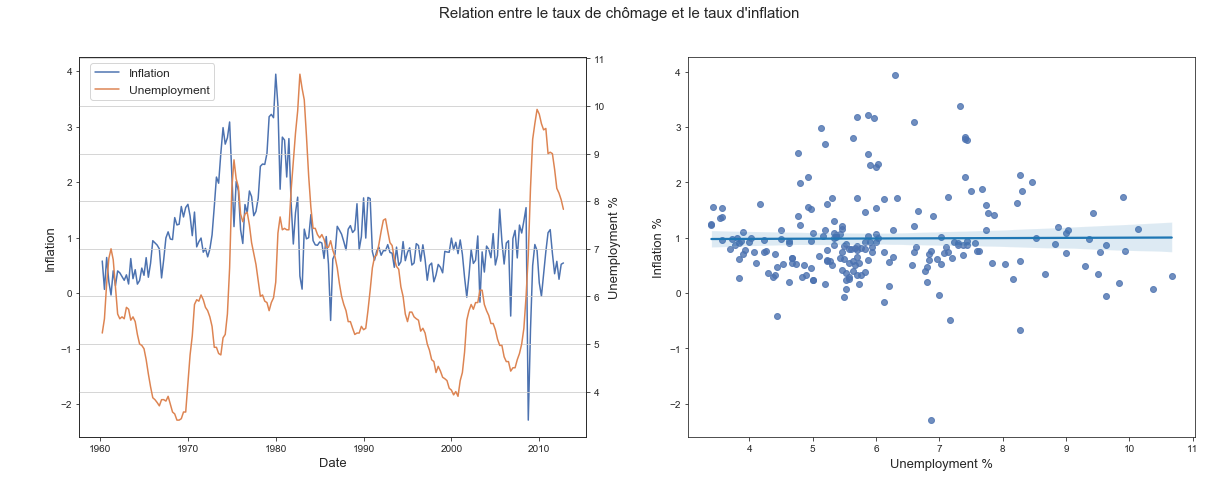
- Regression linéaire
X = sm.add_constant(quarterly.Unemp[1:])
y = inflation.dropna()
model = sm.OLS(y, X)
results = model.fit()
residual = results.resid
display_html(OLS_summary(results))
| parameters | cov | HC3 | p_values | |
|---|---|---|---|---|
| const | 0.9631 | 0.2086 | 0.1590 | 0.000 |
| Unemp | 0.0037 | 0.0331 | 0.0267 | 0.912 |
Sans vérifications des conditions d’optimalités de l’estimateur OLS, on ne peut pas conclure sur l’influence du taux de chomage sur l’inflation. Cependant, même si le coeffcient de la regression se retrouve à être significatif avec des méthodes d’estimation des MCG, cette influence sera faible.
- hétérocsédasticité
Tester l’autocorrélation des erreurs
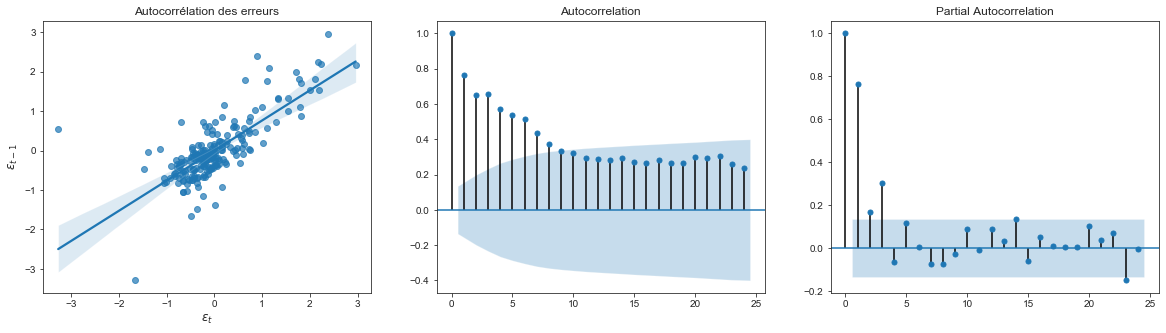
- On remarque une forte autocorrélation des erreurs du modèle. Ceci est frèquent dans l’étude des séries temporelles. Le modèle à tendance à se tromper plus à l’instant $t$ s’il s’est trompé à l’instant $t-1$.
Nous allons appliquer le test de Durbin-Watson pour tester l’autocorrélation des erreurs.
Le modèle considéré est:
\[\epsilon_t = \rho \epsilon_{t-1} + u_t\]Et on teste l’hypothèse nulle:
\[H_0 = \{ \rho = 0 \}\]La statistique de test est:
\[d = \frac{\sum_{t=2}^{T}(\epsilon_t - \epsilon_{t-1})^2}{\sum_{t=1}^{T}\epsilon_t^2} \rightarrow 2(1 - \hat{\rho})\]d = np.sum((residual - residual.shift(1))**2) / np.sum(residual**2)
rho = 1 - d/2
print("Durbin-Watson coefficient: {:.3f}".format(d))
print("rho: {:.3f}".format(rho))
Durbin-Watson coefficient: 0.475
rho: 0.763
La loi asymptotique de cette estimateur n’est pas connue analytiquement mais il existe des tables permettant de tester la significativité du test.
Pour $\bf k=1$ (une variable explicative) avec intercept et $ n=212$:
- $ dl=1.65$ et $ du=1.85$.
- Ici, $\bf d=0.475 < dl$, ainsi, $\bf H_0$ est rejetée. Les résidus sont autocorrélés
Le test d’autocorrélation des résidus peut être réalisé par MCO sur les résidus estimés. Le test de significativité par MCO est valable seulement asymptotiquement. Les deux estimations convergent vers la même valeurs.
| parameters | cov | HC3 | p_values | |
|---|---|---|---|---|
| rho | 0.7624 | 0.0448 | 0.0598 | 0.000 |
On obtient la même estimation de $\rho$ avec une estimation par moindres carrés.
Corriger l’autocorrélation des erreurs
Puisque le taux de chômage à un impact presque nul dans le régression, on remarque que l’autocorrélogramme des résidus est presque identique à celui de l’inflation. La modélisaiton adaptée pour modéliser les résidus est donc un modèle $AR(3)$. Cependant, le premier coefficient d’autocorrélation partiel étant prédominant, on peut se limiter à une modélisation à l’ordre 1 des résidus avec une précision suffisante.
Nous allons corriger l’autocorrélation en appliquant l’OLS sur:
\[\left\{ \begin{array}{l l} \tilde{y} = y_t - \hat{\rho} y_{t-1} \\ \tilde{x} = x_t - \hat{\rho} x_{t-1} \\ \end{array} \right.\]X = sm.add_constant(quarterly.Unemp)
X = X[2:] - rho*sm.add_constant(quarterly.Unemp).shift(1)[2:]
y = (inflation - rho*inflation.shift(1)).dropna()
model = sm.OLS(y, X)
results = model.fit()
display_html(OLS_summary(results))
- On peut vérifier que l’on obtient les mêmes valeurs en utilisant la méthode
GLSARde statsmodel
X = sm.add_constant(quarterly.Unemp[1:])
y = inflation
model = sm.GLSAR(y, X, 1)
display_html(OLS_summary(model.iterative_fit(2)))
| parameters | cov | HC3 | p_values | |
|---|---|---|---|---|
| const | 1.5671 | 0.4624 | 0.5746 | 0.001 |
| Unemp | -0.0947 | 0.0715 | 0.1044 | 0.187 |
- Nous pouvons aussi appliquer la méthode des moindres carrés génréralisés en spécifiant la matrice de covariance des erreurs:
X = sm.add_constant(quarterly.Unemp)[1:]
y = inflation
n, p = X.shape
sigma_hat = np.sum(residual**2) / (n - p)
sigma = rho**toeplitz(np.arange(n))
model = sm.GLS(y, X, sigma=sigma)
results = model.fit()
display_html(OLS_summary(results))
| parameters | cov | HC3 | p_values | |
|---|---|---|---|---|
| const | 1.5206 | 0.4549 | 0.5814 | 0.001 |
| Unemp | -0.0898 | 0.0708 | 0.0837 | 0.206 |
- Vérification du résultat en appliquant la formule de l’estimateur des MCG
from scipy.stats import f, t
# --- computation of beta --- #
a = np.linalg.inv(np.linalg.multi_dot([X.T, np.linalg.inv(sigma), X]))
b = np.linalg.multi_dot([X.T, np.linalg.inv(sigma), y])
beta = a.dot(b)
# --- computation of p-values --- #
residual = y - X.dot(beta)
gram = np.dot(X.T.dot(np.linalg.inv(sigma)), X) / n
sigma_hat = np.sqrt(np.sum(residual**2) / (n - p))
teta_k = beta
s_nk = np.sqrt(np.diag(np.linalg.inv(gram)))
t_stat = np.sqrt(n) / (s_nk * sigma_hat) * teta_k
p_value = t.sf(np.abs(t_stat), n-p)*2
pd.DataFrame(np.round(np.vstack((beta, p_value)).T, 4) , index=X.columns, columns=["parameters", "p-values"])
| parameters | p-values | |
|---|---|---|
| const | 1.5206 | 0.0013 |
| Unemp | -0.0898 | 0.2161 |
- Nous avons vu que les méthodes OLS avec variables sphéricisée et GLM sont équivalentes. La transformation permettant de sphériciser les variables est la décomposition de Cholesky de la matrice de covariance $\Omega$.
Tester la stabilité de la relation chômage-inflation sur deux sous-périodes de taille identique
X = sm.add_constant(quarterly.Unemp)[1:]
y = inflation
n, p = X.shape
ind = n // 2
sigma = rho**toeplitz(np.arange(n))
model = sm.GLS(y, X, sigma=sigma)
results = model.fit()
SSE_c = np.sum(results.resid**2)
# -- regression for the first division -- #
X1 = X[:ind]
y1 = inflation.dropna()[:ind]
sigma = rho**toeplitz(np.arange(ind))
model = sm.GLS(y1, X1, sigma=sigma)
results = model.fit()
SSE1 = np.sum(results.resid**2)
# -- regression for the second division -- #
X2 = X[ind:]
y2 = inflation.dropna()[ind:]
sigma = rho**toeplitz(np.arange(n - ind))
model = sm.GLS(y2, X2, sigma=sigma)
results = model.fit()
SSE2 = np.sum(results.resid**2)
f_stat = ((SSE_c-(SSE1+SSE2)) / p) / ((SSE1+SSE2)/(n-2*p))
p_value = f.sf(f_stat, p, n-2*p)
display_html(pd.DataFrame({"f-stat": f_stat, "p-value": p_value}, index=["results"])\
.style.format({'f-stat': "{:.3f}", 'p-value': "{:.3f}"}))
| f-stat | p-value | |
|---|---|---|
| results | 10.046 | 0.000 |
Le test de changement de strucute est significatif. On accepte donc l’hypothèse de changement de structure entre les deux sous groupes.
Faites les tests changement de structure de Chow et détecter le point de rupture
def regression_over_period(ind: int):
# -- regression for the first division -- #
X1 = X[:ind]
y1 = inflation.dropna()[:ind]
sigma = rho**toeplitz(np.arange(ind))
model = sm.GLS(y1, X1, sigma=sigma)
results = model.fit()
SSE1 = np.sum(results.resid**2)
# -- regression for the second division -- #
X2 = X[ind:]
y2 = inflation.dropna()[ind:]
sigma = rho**toeplitz(np.arange(n - ind))
model = sm.GLS(y2, X2, sigma=sigma)
results = model.fit()
SSE2 = np.sum(results.resid**2)
return SSE1, SSE2
plt.figure(figsize=(12, 7))
fisher = []
for ind in range(50, 150):
SSE1, SSE2 = regression_over_period(ind)
fisher.append( ((SSE_c-(SSE1+SSE2)) / p) / ((SSE1+SSE2)/(n-p)))
plt.plot(quarterly.DATE[50:150], fisher)
plt.title("Test de Chow pour différent valeur t de changement de structure")
plt.xlabel("periode de changement de structure")
plt.ylabel("test de Fisher")
plt.grid()
plt.show()
print(f"Changement de structure le plus significatif: {quarterly.DATE[np.argmax(fisher)+50]}")
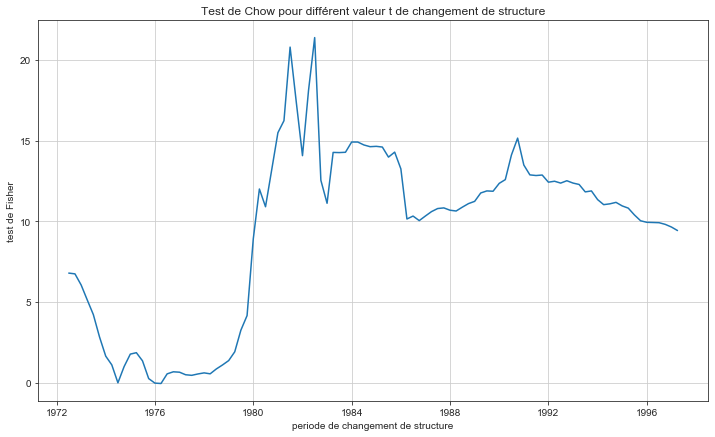
Changement de structure le plus significatif: 1982-07-01 00:00:00
- Ce changement de structure correspond à 3ème trimestre de 1982, l’année succédant la fin du choc pétrolier pendant lequelles le prix du baril a été multiplié par 2.7.
Estimer la courbe de Philips en supprimant l’inflation courante des variables explicatives mais en ajoutant les délais d’ordre 1, 2, 3 et 4 de l’inflation et du chômage. Faire le test de Granger de non causalité de l’inflation sur le chômage
X = pd.concat([pd.concat([inflation.shift(i) for i in range(1, 5)], axis=1), pd.concat([quarterly.Unemp.shift(i) for i in range(1, 5)], axis=1)], axis=1)
new_names = []
for i, name in enumerate(X.columns):
new_names.append(name + '_' + str((i%4+1)))
X.columns = new_names
X = X[5:]
X = sm.add_constant(X)
X.head(2)
| const | inf_1 | inf_2 | inf_3 | inf_4 | Unemp_1 | Unemp_2 | Unemp_3 | Unemp_4 | |
|---|---|---|---|---|---|---|---|---|---|
| 5 | 1.0 | 0.201478 | 0.642109 | 0.067636 | 0.578231 | 6.8 | 6.27 | 5.53 | 5.23 |
| 6 | 1.0 | -0.033512 | 0.201478 | 0.642109 | 0.067636 | 7.0 | 6.80 | 6.27 | 5.53 |
- Test de causalité de Granger
Nous allons appliquer le test de Fisher de nullité des coefficient associés à $Unemp$ dans la régression de:
\[inf_t = \beta_0 + \beta_{inf_1}inf_{t-1}+ \beta_{inf_2}inf_{t-2}+ \beta_{inf_3}inf_{t-3}+ \beta_{inf_4}inf_{t-4} + \beta_{Unemp_1}Unemp_{t-1}+ \beta_{Unemp_2}Unemp_{t-2}+ \beta_{Unemp_3}Unemp_{t-3}+ \beta_{Unemp_4}Unemp_{t-4}\]# --- regression with all variables --- #
y = inflation[4:]
n, p = X.shape
model = sm.OLS(y, X)
results = model.fit()
residual = results.resid
SSE = np.sum(residual**2)
# --- regression without Unemp variable (beta_Unemp_i = 0 in the f-test) --- #
X1 = X.iloc[:, :5]
y = inflation[4:]
model = sm.OLS(y, X1)
results1 = model.fit()
residual1 = results1.resid
SSE1 = np.sum(residual1**2)
# --- Compute Fisher Stat --- #
f_stat = ((SSE1 - SSE) / 4) / (SSE / (n - 4))
p_value = f.sf(f_stat, 4, n - 4)
results_fisher = pd.DataFrame({"f-stat": f_stat, "p-value": p_value}, index=["results"])\
.style.format({'f-stat': "{:.3f}", 'p-value': "{:.3f}"})
display_html(results_fisher)
display_html(OLS_summary(results))
| f-stat | p-value | |
|---|---|---|
| results | 5.011 | 0.001 |
| parameters | cov | HC3 | p_values | |
|---|---|---|---|---|
| const | 0.2914 | 0.1371 | 0.1137 | 0.035 |
| inf_1 | 0.5697 | 0.0712 | 0.1018 | 0.000 |
| inf_2 | 0.0095 | 0.0775 | 0.1334 | 0.903 |
| inf_3 | 0.3223 | 0.0756 | 0.2115 | 0.000 |
| inf_4 | 0.0048 | 0.0712 | 0.1209 | 0.946 |
| Unemp_1 | -0.5900 | 0.1349 | 0.2113 | 0.000 |
| Unemp_2 | 0.8765 | 0.2539 | 0.3232 | 0.001 |
| Unemp_3 | -0.3150 | 0.2567 | 0.3402 | 0.221 |
| Unemp_4 | -0.0036 | 0.1331 | 0.1407 | 0.978 |
- La p-valeur du test de fisher est 0.001, on rejette l’hypothèse nulle de non significativité globale des coefficient. On peut ainsi dire au sens de Granger qu’il y a une relation de causalité du chômage sur l’inflation.
Représentez graphiquement les délais distribués et commentez. Calculer l’impact à long terme de l’inflation sur le chômage
fig, ax = plt.subplots(1, 2, figsize=(16, 5))
ax[0].stem(range(1, 5), results.params[1:5], use_line_collection=True)
ax[0].set_title("Coefficients associés à l'inflation en fonction du délais dans la regression", fontsize=12)
ax[0].set_xlabel("Délais inflation", fontsize=12)
ax[0].set_xticks(range(1, 5))
ax[1].stem(range(1, 5), results.params[5:], use_line_collection=True)
ax[1].set_title("Coefficients associés au taux de chomage en fonction du délais dans la regression", fontsize=12)
ax[1].set_xlabel("Délais chomage", fontsize=12)
ax[1].set_xticks(range(1, 5))
plt.show()
print("Somme des coefficients associés au taux de chomage: {0:0.3f}".format(np.sum(results.params[5:])))
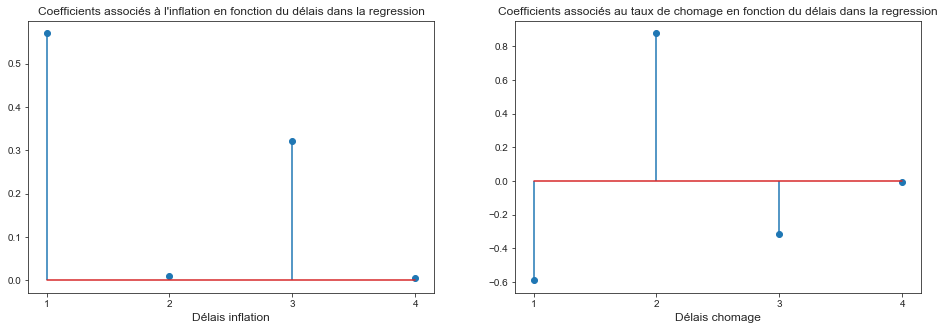
Somme des coefficients associés au taux de chomage: -0.032
-
Les délais coefficient de la regression associé aux délais distribués de l’inflation suivent la même tendance son l’autocorrélogramme. Ceux associés au taux de chômage suivent la tendance d’un modèle AR à coefficients négatif.
-
Sur le long terme, si on considère que le taux de chomage est stable sur 3 trimestres, puisque $\sum_{i=1}^{4} \theta_{Unemp-i} = -0.032$ on peut dire que sur le long terme, le taux de chômage n’a pas d’influence sur le taux d’intérêt. Une hausse de 1 point de l’inflation entraîne une baisse de 0.03 point du taux de chomage. C’est la vision monétariste de la courbe de Phillips.
