Économétrie
01 April 2020
Régression linéaire et hétéroscédasticité
Cette page présente un projet d’économétrie réalisé pendant mon année à Télécom Paris. Les données proviennent du jeu de données Mroz contenant des informations sur la participation des femmes dans l’économie Américaine dans les années 2000.
Le but du projet est dans un premier temps de réaliser des tests d’hypothèses sur les coefficients de régression du salaire sur plusieurs varibles puis d’analyser les sources d’hétéroscédasticité du modèle afin de les corriger. La correction de l’hétéroscédasticité permet d’avoir des estimateurs efficients en sphériscisant la matrice de covariance des bruits (théorème de Gauss Markov)
Jeu de donnée
| inlf | hours | kidslt6 | kidsge6 | age | educ | wage | repwage | hushrs | husage | ... | faminc | mtr | motheduc | fatheduc | unem | city | exper | nwifeinc | lwage | expersq | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1610 | 1 | 0 | 32 | 12 | 3.3540 | 2.65 | 2708 | 34 | ... | 16310 | 0.7215 | 12 | 7 | 5.0 | 0 | 14 | 10.91006 | 1.210154 | 196 |
| 1 | 1 | 1656 | 0 | 2 | 30 | 12 | 1.3889 | 2.65 | 2310 | 30 | ... | 21800 | 0.6615 | 7 | 7 | 11.0 | 1 | 5 | 19.49998 | 0.328512 | 25 |
Calculer les corrélations motheduc et fatheduc. Expliquer le problème de multi-collinéarité
corr = mroz.loc[:, ['motheduc', 'fatheduc']].corr()
plt.figure(figsize=(5, 4))
sns.heatmap(corr, annot=True, cmap=sns.color_palette("Blues"))
plt.show()
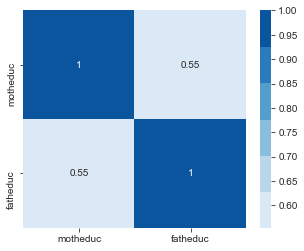
Si la matrice de design $\mathbf{X}$ présente des colonnes colinéaires entre elles, ceci peut entrainer des problèmes de conditionnement pour l’inversion de la matrice $\mathbf{X^TX}$. Le vrai ploblème cependant réside dans l’explosion de la variance des estimateurs des paramêtres de la regression: $ V(\theta) = \sigma (X^TX)^{-1} $
Faites un graphique en nuage de point entre wage et educ. S’agit-il d’un effet “toute chose étant égale par ailleurs ?”
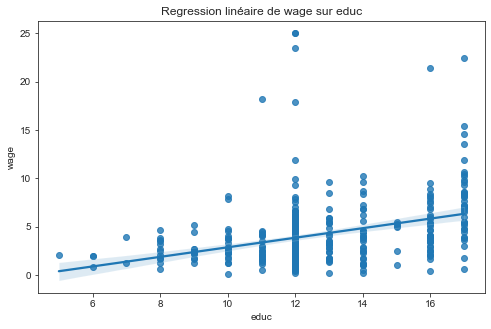
On constate une corrélation positive entre le niveau d’éducation et le salaire. On ne peut cependant pas dire facilement comme souvent en économétrie que cet effet soit un effet “toute chose étant égale par ailleurs”. Il se pourrait par exemple que le niveau d’éducation dépende majoritairement de la classe sociale des individus. Ainsi, la corrélation que l’on constate ici ne serait en fait due qu’a la classe sociale et non au niveau d’éduction qui en dépend.
Quelle est l’hypothèse fondamentale qui garantit des estimateurs non biaisés ? Expliquer le biais de variable omise
L’hypothèse fondamentale garantissant des estimateurs non biaisés est que les résidus $\bf\epsilon$ du modèles sont indépendant des variables explicatives i.e:
\[E(\epsilon | x) = 0\]En effet, l’estimateur des MCO s’écrit:
\[\begin{align} \hat{\theta} &= (X^tX)^{-1}X^tY \\ &= (X^tX)^{-1}X^t(X\theta^* + \epsilon) \\ &= \theta^* + (X^tX)^{-1}X^t\epsilon \end{align}\]En rappelant que \(E_{x, y}[f(x, y)] = E_xE_y[f(x, y) \mid x]\) et qu’un estimateur \(\hat{m}\) est sans biais ssi \(E_{x, y}[\hat{m}(x, y)]=0\)
\[\begin{align*} E_{x, y}[\hat{\theta}(y, x) \mid x)] &= \theta^* + (X^tX)^{-1} X^t E[\epsilon \mid x]\\ &= 0 \ \text{si} \ E[\epsilon | x]=0 \end{align*}\]Le biais de variable omise survient lorsqu’une des variables explicatives corrélée à la fois avec la variable expliquée et avec le terme d’erreur n’est pas prise en compte dans l’équation. Dans ce cas, l’hypothèse fondamentale garantissant que les estimateurs MCO sont non biaisé n’est plus valide.
Faire la régression du log de wage en utilisant comme variables explicatives une constante, city, educ, exper, nwifeinc, kidslt6, kidsgt6
X = sm.add_constant(mroz[["city", "educ", "exper", "nwifeinc", "kidslt6", "kidsge6"]])
y = mroz["lwage"]
main_model = sm.OLS(y, X)
main_results = main_model.fit()
main_residual = main_results.resid
display_html(OLS_summary(main_results))
plt.figure(figsize=(7, 4))
sns.distplot(main_residual)
plt.title("Résidus du modèle", fontsize=14)
plt.show()
| parameters | cov | HC3 | p_values | |
|---|---|---|---|---|
| const | -0.3990 | 0.2071 | 0.2008 | 0.055 |
| city | 0.0353 | 0.0702 | 0.0687 | 0.616 |
| educ | 0.1022 | 0.0151 | 0.0143 | 0.000 |
| exper | 0.0155 | 0.0045 | 0.0045 | 0.001 |
| nwifeinc | 0.0049 | 0.0033 | 0.0029 | 0.143 |
| kidslt6 | -0.0453 | 0.0853 | 0.1043 | 0.596 |
| kidsge6 | -0.0117 | 0.0269 | 0.0287 | 0.664 |
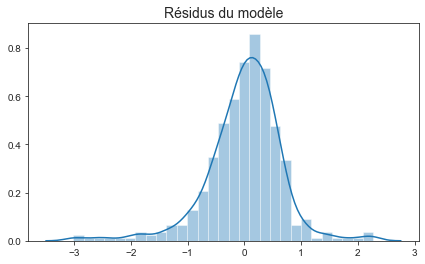
Nous rappelons ici le théorème de cochran qui montre que sous l’hypothèse de bruit Gaussien, les coefficients de la régression linéaire suivent une loi de student:
Sous l’hypothèse de bruit de modèle Gaussien:
\[\left( \frac {n^{1 / 2}} {\hat{s}_{n, k}^{1/2} \hat{\sigma}_{n}} (\hat{\boldsymbol{\theta}}_{k}-\boldsymbol{\theta}_{k}^{*})\right) \sim \mathcal{T}_{n-p-1}\]où $ T_{n-p-1} $ est la distribution de Student avec $n-p-1$ degrées de libertés.
L’histogramme des résidus semble être gaussien. L’hypothèse des bruits gaussiens permet d’utiliser la statistique de Student non asymptotiquement.
Tester l’hypothèse de non significativité de nwifeinc avec un seuil de significativité de 1%, 5% et 10% (test alternatif des deux côtés)
- Test de student pour la significativité de nwifeinc:
- Ici,
- Donc, sous cette hypothèse:
n, p = X.shape
gram = X.T.dot(X) / n
sigma_hat = np.sqrt(np.sum(main_residual**2) / (n - p))
teta_k = main_results.params["nwifeinc"]
s_nk = np.sqrt(pd.DataFrame(np.linalg.inv(gram), gram.columns, gram.index).loc["nwifeinc", "nwifeinc"])
t_stat = np.sqrt(n) / (s_nk * sigma_hat) * teta_k
p_value = t.sf(t_stat, n-p)*2
display_html(pd.DataFrame({"t-stat": t_stat, "p-value": p_value}, index=["results"])\
.style.format({'t-stat': "{:.3f}", 'p-value': "{:.3f}"}))
| t-stat | p-value | |
|---|---|---|
| results | 1.466 | 0.143 |
La p-valeur du test de student est 0.143. Cela signifie que la probabilité d’obtenir un coefficient au moins aussi grand que celui obtenu sous l’hypothèse nulle est 0.143, i.e $ P(\theta_{nwifeinc} = 0 \mid | \hat{\theta}_{nwifeinc} | > 0.0049) = {\bf 0.143} $. Ainsi, les hypothèses aux seuils 1%, 5%, 10% ne peuvent donc pas être rejettées.
Tester l’hypothèse que le coefficient associé à nwifeinc est égal à 0.01 avec un seuil de significativité de 5% (test à alternatif des deux côtés)
- On reprend le test de Student de la quesiton précédente sauf que le test ici est:
- Sous cette hypothèse,
t_stat = np.sqrt(n) / (s_nk * sigma_hat) * (teta_k - 0.01)
p_value = t.sf(np.abs(t_stat), n-p)*2
display_html(pd.DataFrame({"t-stat": np.abs(t_stat), "p-value": p_value}, index=["results"])\
.style.format({'t-stat': "{:.3f}", 'p-value': "{:.3f}"}))
| t-stat | p-value | |
|---|---|---|
| results | 1.536 | 0.125 |
- La p-value du test est de 0.125, le test de significativité à 5% n’est donc pas rejetté.
Tester l’hypothèse jointe que le coefficient de nwifeinc est égal à 0.01 et que celui de city est égal à 0.05
Le modèle initial est:
\[log(wage) = \beta_0 + \beta_{city} city + {\bf \beta_{educ}} educ + \beta_{exper} exper + {\bf \beta_{nwifeinc}} nwifeinc + \beta_{kedslt} kedslt + \beta_{kidsgt} kidsgt\]On souhaite à présent tester
\[H_0 : \{ \beta_{nwifeinc}=0.01, \beta_{city}=0.05 \}\]Nous allons donc appliquer le test de Fisher au modèle:
\[log(wage) - {\bf0.05} \ city - {\bf0.01} \ nwifeinc = \beta_0 + \beta_{educ} educ + \beta_{exper} exper + {\bf \beta_{nwifeinc}} nwifeinc + \beta_{kedslt} kedslt + \beta_{kidsgt} kidsgt\]Le statistique de Fisher associé a ces deux modèles est:
\[f_{stat} = \frac{\frac{(SSE_1 - SSE)}{2}} {\frac{SSE}{n - p - 1}}\]# --- fit linear regression model with all variables --- #
X = sm.add_constant(mroz[["city", "educ", "exper", "nwifeinc", "kidslt6", "kidsge6"]])
y = mroz["lwage"]
n, p = X.shape
model = sm.OLS(y, X)
results = model.fit()
residual = results.resid
SSE = np.sum(residual**2)
# --- fit regression model with 2 constraints on beta coefficients --- #
X = sm.add_constant(mroz[["educ", "exper", "kidslt6", "kidsge6"]])
y = mroz["lwage"] - 0.05*mroz["city"] - 0.01*mroz["nwifeinc"]
model = sm.OLS(y, X)
results = model.fit()
residual = results.resid
SSE1 = np.sum(residual**2)
# --- Compute Fisher Stat --- #
f_stat = ((SSE1 - SSE) / 2) / (SSE / (n - p))
p_value = f.sf(f_stat, 2, n - p)
display_html(pd.DataFrame({"f-stat": f_stat, "p-value": p_value}, index=["results"])\
.style.format({'f-stat': "{:.3f}", 'p-value': "{:.3f}"}))
| f-stat | p-value | |
|---|---|---|
| results | 1.337 | 0.264 |
- La p-valeur du test est $\bf 0.26$, l’hypothèse $ H_0 : { \beta_{nwifeinc}=0.01, \beta_{city}=0.05 }$ est donc acceptée.
Tester l’hypothèse jointe que ${ \beta_{nwifeinc} + \beta_{city} =0.1 }$ et $\bf { \beta_{educ} + \beta_{exper} =0.1 } $
Les deux conditions du modèle restreint sont:
\[\left\{ \begin{array}{l l} \beta_{nwifeinc} &= 0.1 - \beta_{city} & \quad \\ \beta_{educ} &= 0.1 - \beta_{exper} & \quad \\ \end{array} \right.\]Nous allons donc appliquer le test de Fisher au modèle:
\[log(wage) - {\bf0.1} \ mwifeinc - {\bf0.1} \ educ = \beta_0 + \beta_{city} {\bf (city - nwifeinc)} + \beta_{exper} {\bf (exper - educ)} + \beta_{kedslt} kedslt + \beta_{kidsgt} kidsgt\]Le statistique de Fisher associé a ces deux modèles est:
\[f_{stat} = \frac{\frac{(SSE_1 - SSE)}{2}} {\frac{SSE}{n - p - 1}}\]# --- fit linear regression model with all variables --- #
X = sm.add_constant(mroz[["city", "educ", "exper", "nwifeinc", "kidslt6", "kidsge6"]])
y = mroz["lwage"]
n, p = X.shape
model = sm.OLS(y, X)
results = model.fit()
residual = results.resid
SSE = np.sum(residual**2)
# --- fit regression model with 2 constraints on beta coefficients --- #
X = sm.add_constant(mroz[["kidslt6", "kidsge6"]])
X["city_nwfeinc"] = mroz["city"] - mroz["nwifeinc"]
X["exper_educ"] = mroz["exper"] - mroz["educ"]
y = mroz["lwage"] - 0.1*mroz["educ"] - 0.1*mroz["nwifeinc"]
model = sm.OLS(y, X)
results = model.fit()
residual = results.resid
SSE1 = np.sum(residual**2)
# --- Compute Fisher Stat --- #
f_stat = ((SSE1 - SSE) / 2) / (SSE / (n - p))
p_value = f.sf(f_stat, 2, n - p)
display_html(pd.DataFrame({"f-stat": f_stat, "p-value": p_value}, index=["results"])\
.style.format({'f-stat': "{:.3f}", 'p-value': "{:.3f}"}))
| f-stat | p-value | |
|---|---|---|
| results | 0.923 | 0.398 |
La p-valeur du test est $\bf 0.398$, l’hypothèse \(H_0 : \big\{ \bf \{ \beta_{nwifeinc} + \beta_{city} =0.1 \}\) et \(\bf \{ \beta_{educ} + \beta_{exper} =0.1 \} \big\}\) est donc acceptée.
Faites une représentation graphique de la manière dont le salaire augmente avec l’éducation et l’expérience professionnelle
- Le graphique proposé trace le salaire en fonction de l’expérience pour deux niveaux d’éducation, inférieur et au dessus de la médiane (12 années).
df = mroz.copy()
df["educ>=12"] = df.educ >= 12
_, axes = plt.subplots(1, 2, figsize=(22, 7))
with sns.plotting_context(rc={"legend.fontsize":13}):
sns.lineplot(x="exper", y="wage", hue="educ>=12", data=df, palette=sns.diverging_palette(253, 18, 99, 64, 1, 2), ax=axes[0])
plt.xlabel("exper", fontsize=13)
plt.ylabel("wage", fontsize=13)
sns.lineplot(x="exper", y="repwage", hue="educ>=12", data=df, palette=sns.diverging_palette(253, 18, 99, 64, 1, 2), ax=axes[1])
plt.xlabel("exper", fontsize=13)
plt.ylabel("repwage", fontsize=13)
axes[0].set_title("Evolution du salaire/(heure travaillée) en fonction du niveau d'éducation et de l'expérience", fontsize=14)
axes[1].set_title("Evolution du salaire en fonction du niveau d'éducation et de l'expérience", fontsize=14)
plt.show()
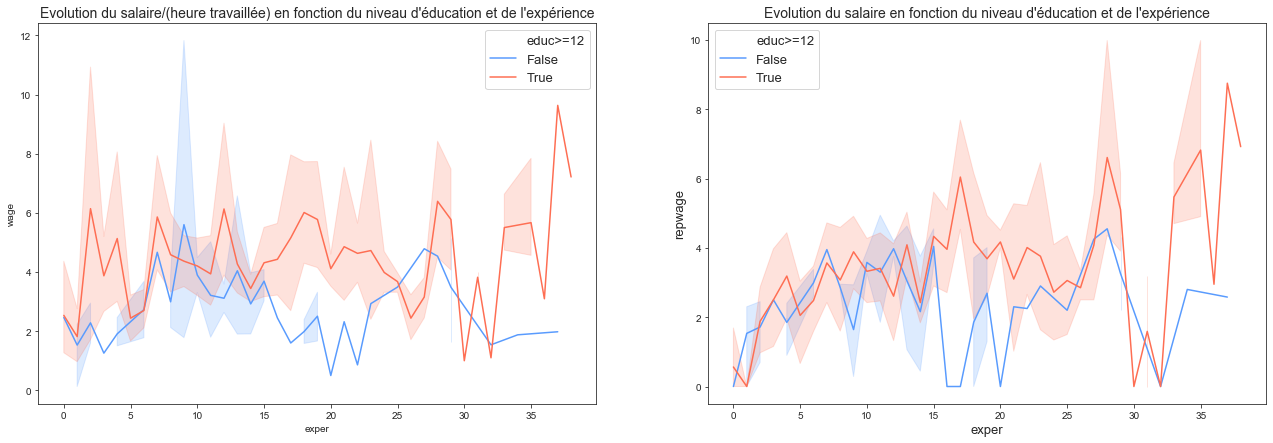
On voit que le niveau d’éducation à une forte influence sur le salaire en début et fin de carrière. Autour de 10 ans d’expérience, l’éducation a moins d’influence.
Globalement, pour des niveaux d’éducation supérieurs à 12 années, le salaire croit avec l’expérience contrairement à celui des personnes ayant des niveaux d’expériences inférieurs pour lesquels leurs salaires reste constant au cours de leurs carrières. Ce derniers point s’explique par le fait que les personnes les moins qualifiées sont sujet à avoir des métiers précaires et ne peuvent pas forcément capitaliser sur l’expérience gagnée dans leurs métiers.
Faire le test d’hétéroscédasticité de forme linéaire en donnant la p-valeur. Déterminer la ou les sources d’hétéroscédasticité.
- Avant toute chose, trançons les résidus en fonction de certaines varibles de la régression.
df = mroz.copy()
X = sm.add_constant(mroz[["city", "educ", "exper", "nwifeinc", "kidslt6", "kidsge6"]])
df["y_hat"] = main_results.predict(X)
_, axes = plt.subplots(2, 3, figsize=(20, 10))
col_names = [["y_hat", "exper", "educ"], ["nwifeinc", "city", "kidslt6"]]
window_sizes = [[0.2, 3, 2], [6, 0.5, 0.5]]
for i in range(axes.shape[0]):
for j in range(axes.shape[1]):
plot_residual_vs_variable(df, main_residual, col_names[i][j], window_sizes[i][j], axes[i][j])
plt.show()
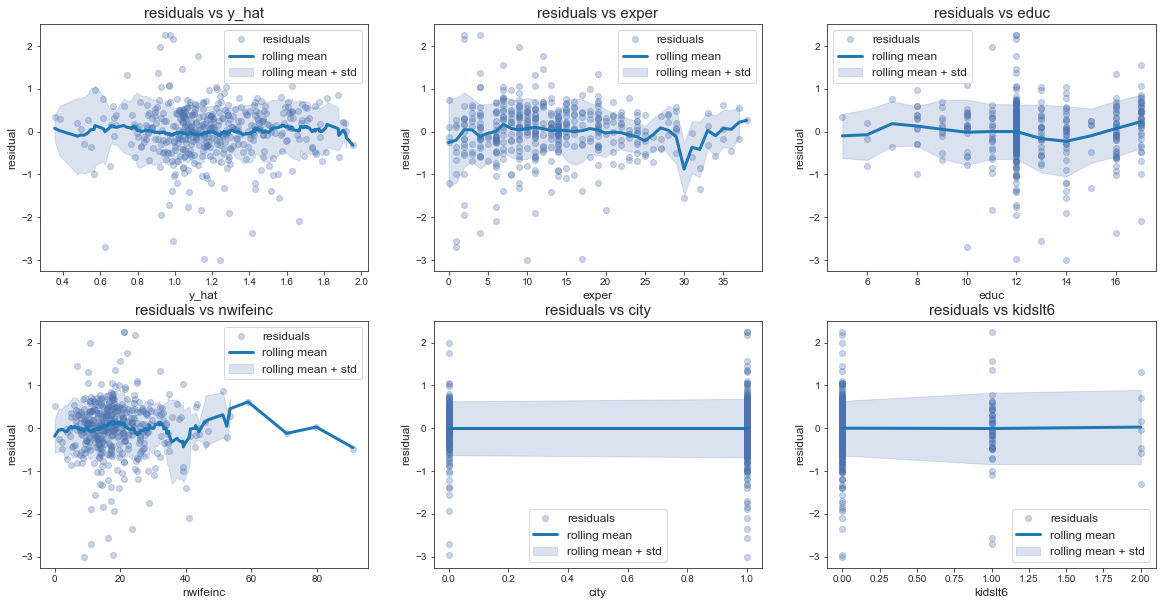
- Il semble difficile d’évaluer les sources d’hétéroscédasticité de façon qualitative ici, nous allons appliquer le test de Fisher sur la nullité des coefficient de la regression des variables explicatives sur la norme euclidienne des résidus:
Le test de nullité des coefficients est:
\[H_0 : \{ \beta_{i}=0, \forall i>1 \}\] \[f_{stat} = \frac{\frac{(SSE_1 - SSE)}{6}} {\frac{SSE}{n - p - 1}}\]X = sm.add_constant(mroz[["city", "educ", "exper", "nwifeinc", "kidslt6", "kidsge6"]])
y = mroz["lwage"]
n, p = X.shape
model = sm.OLS(y, X)
results = model.fit()
residual = results.resid
model = sm.OLS(residual**2, X)
results_heter = model.fit()
SSE = np.sum(results_heter.resid**2)
SSE1 = np.var(residual**2) * n
# --- Compute Fisher Stat --- #
f_stat = ((SSE1 - SSE) / 6) / (SSE / (n - p))
p_value = f.sf(f_stat, 6, n - p)
results_fisher = pd.DataFrame({"f-stat": f_stat, "p-value": p_value}, index=["results"])\
.style.format({'f-stat': "{:.3f}", 'p-value': "{:.3f}"})
display_html(results_fisher)
display_html(OLS_summary(results_heter))
| f-stat | p-value | |
|---|---|---|
| results | 2.009 | 0.063 |
| parameters | cov | HC3 | p_values | |
|---|---|---|---|---|
| const | 0.4519 | 0.3231 | 0.2885 | 0.163 |
| city | 0.0967 | 0.1095 | 0.1119 | 0.378 |
| educ | 0.0126 | 0.0236 | 0.0195 | 0.593 |
| exper | -0.0170 | 0.0070 | 0.0066 | 0.016 |
| nwifeinc | -0.0036 | 0.0052 | 0.0043 | 0.495 |
| kidslt6 | 0.1279 | 0.1331 | 0.1556 | 0.337 |
| kidsge6 | 0.0278 | 0.0420 | 0.0332 | 0.509 |
- La p-valeur du test d’hétéroscédasticité de forme linéaire est 0.063. Il existe certainement des source d’hétéroscédasticité même si l’hypothèse $ H_0 : { \beta_{i}=0, \forall i>1 }$ est acceptée au risque 5%. En testant l’hétéroscédasticité coefficient par coefficient avec un test de Student, on remarque que la variable exper est significative (p-valeur de 0.016) avec un coefficient associé tout de même assez faible (-0.017). En prettant plus d’attention à la courbe des résidus en fonction de l’expérience, on devrait remarquer une tendance légèrement baissière de la variance des résidus.
Retraçons les moyennes mobiles des résidus sur une fenètre de 5 années en fonction de l’expérience:
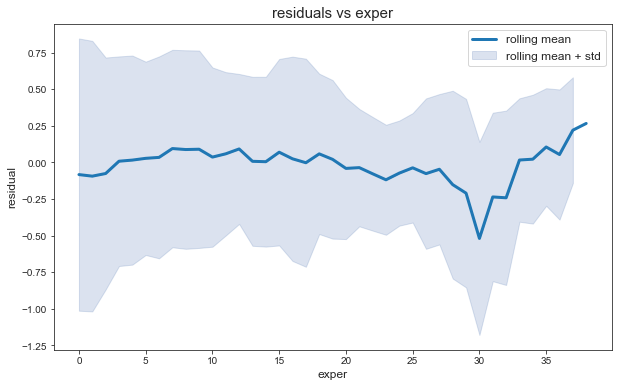
On remarque en effet une légère tendance baissière des de la variance des résidus en fonction de l’expérience.
- Remarquons tout d’abord que l’effet de taille lié au salaire à déjà été retiré en appliquant la regression linéaire au logarithme du salaire.
- Une technique permettant de corriger l’hétéroscédasticité est d’utiliser la méthode des moindres carrés généralisés (MCG). Ici, nous n’avons pas de connaissance à priori sur la matrice de variance $\Omega$ des pertubations. Nous allons donc utiliser la méthode des Moindres Carrés Quasi-Généralisés (MCQG) qui conciste à remplacer la vrai matrice de covariance par son estimateur.
- On peut alors soit estimer la matrice $\Omega$ avec l’estimateur robuste de White soit utiliser la méthode moins générale des Moindres carrés pondérés qui conciste à disposer d’informations supplémentaires sur la forme de l’hétéroscédasticité.
Nous allons utiliser ici la méthode des Mondres carrés pondérés qui conciste à réaliser les étapes suivantes:
- Estimer la régression $Y=X \beta+\varepsilon$ par MCO.
- Utiliser des résidus $\widehat{\varepsilon}$ et calculer $\log \left(\epsilon_{i}^{2}\right)$
- Estimer la régression $\log \left(\epsilon_{i}^{2}\right)=\alpha_{0}+\alpha_{1} X_{1, i}+\ldots+\alpha_{m} X_{p, i}+v_{i}$ et calculer les prédictions $\log \left(\epsilon_{i}^{2}\right).$ (L’exponentielle permet de s’assurer que les écarts types estimés sont positifs).
- Prendre l’exposant des valeurs estimées: $\hat{h}{i}=\exp (\widehat{\log \left(\epsilon{i}^{2}\right)})$
- Estimer $Y=X \beta+\varepsilon$ par MCP avec les poids $\omega_{i}^{-1}=1 / \sqrt{\hat{h}_{i}}$
# --- estimation des coefficients de la régression log(eps^2) --- #
X = sm.add_constant(mroz[["city", "educ", "exper", "nwifeinc", "kidslt6", "kidsge6"]])
y = np.log(main_residual**2)
n, p = X.shape
model = sm.OLS(y, X)
results = model.fit()
log_eps_hat = results.predict(X)
h = np.exp(log_eps_hat)
X = sm.add_constant(mroz[["city", "educ", "exper", "nwifeinc", "kidslt6", "kidsge6"]]).apply(lambda x: x / np.sqrt(h))
y = mroz["lwage"] / np.sqrt(h)
model = sm.OLS(y, X)
results = model.fit()
residual = results.resid
- Comparaison des résidus en fonction de l’expérience pour la régression OLS et WLS
_, (ax1, ax2) = plt.subplots(1, 2, figsize=(20, 6))
plot_residual_vs_variable(df, main_residual, "exper", 5, ax1, show_points=False)
ax1.set_title('residual vs exper OLS')
plot_residual_vs_variable(df, residual, "exper", 5, ax2, show_points=False)
ax2.set_title('residual vs exper WLS')
plt.show()
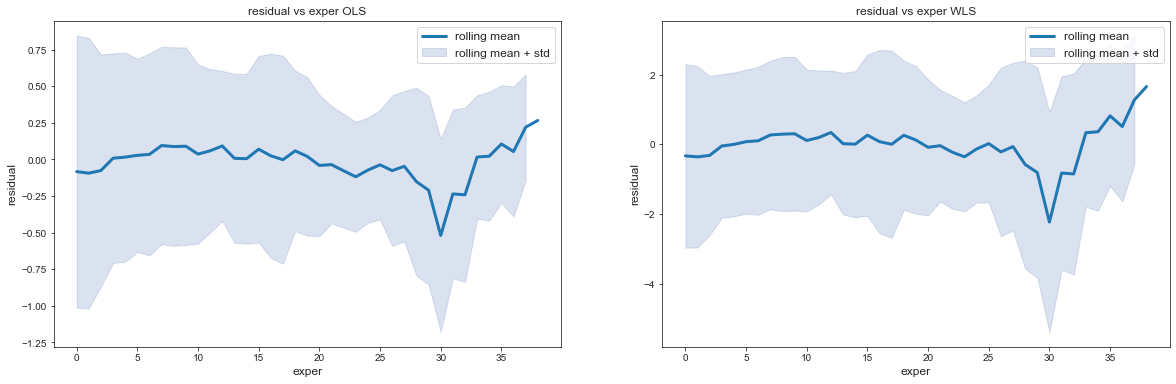
On voit que l’hétéroscédasticité du modèle a été améliorée.
- Comparaison des résultas entre OLS et WLS
titles = ["OLS regression", "WLS regression"]
display_side_by_side_2(titles, OLS_summary(main_results).render(), OLS_summary(results).render())
OLS regression
| parameters | cov | HC3 | p_values | |
|---|---|---|---|---|
| const | -0.3990 | 0.2071 | 0.2008 | 0.055 |
| city | 0.0353 | 0.0702 | 0.0687 | 0.616 |
| educ | 0.1022 | 0.0151 | 0.0143 | 0.000 |
| exper | 0.0155 | 0.0045 | 0.0045 | 0.001 |
| nwifeinc | 0.0049 | 0.0033 | 0.0029 | 0.143 |
| kidslt6 | -0.0453 | 0.0853 | 0.1043 | 0.596 |
| kidsge6 | -0.0117 | 0.0269 | 0.0287 | 0.664 |
WLS regression
| parameters | cov | HC3 | p_values | |
|---|---|---|---|---|
| const | -0.3657 | 0.1875 | 0.1883 | 0.052 |
| city | 0.0196 | 0.0641 | 0.0657 | 0.760 |
| educ | 0.1015 | 0.0138 | 0.0132 | 0.000 |
| exper | 0.0129 | 0.0039 | 0.0042 | 0.001 |
| nwifeinc | 0.0067 | 0.0031 | 0.0025 | 0.031 |
| kidslt6 | -0.0537 | 0.0954 | 0.0896 | 0.574 |
| kidsge6 | -0.0198 | 0.0283 | 0.0277 | 0.484 |
- Comparaison des tests d’hétéroscédasticités
model = sm.OLS(residual**2, X)
results = model.fit()
SSE = np.sum(results.resid**2)
model2 = sm.OLS(residual**2, X.iloc[:, 0:1])
results2 = model2.fit()
SSE1 = np.sum(results2.resid**2)
# --- Compute Fisher Stat --- #
f_stat = ((SSE1 - SSE) / 6) / (SSE / (n - p))
p_value = f.sf(f_stat, 6, n - p)
results_fisher_2 = pd.DataFrame({"f-stat": f_stat, "p-value": p_value}, index=["results"])\
.style.format({'f-stat': "{:.3f}", 'p-value': "{:.3f}"})
display_side_by_side_2(titles, results_fisher.render(), results_fisher_2.render())
display_side_by_side_2(titles, OLS_summary(results_heter).render(), OLS_summary(results).render())
OLS regression
| f-stat | p-value | |
|---|---|---|
| results | 2.009 | 0.063 |
WLS regression
| f-stat | p-value | |
|---|---|---|
| results | 0.465 | 0.834 |
OLS regression
| parameters | cov | HC3 | p_values | |
|---|---|---|---|---|
| const | 0.4519 | 0.3231 | 0.2885 | 0.163 |
| city | 0.0967 | 0.1095 | 0.1119 | 0.378 |
| educ | 0.0126 | 0.0236 | 0.0195 | 0.593 |
| exper | -0.0170 | 0.0070 | 0.0066 | 0.016 |
| nwifeinc | -0.0036 | 0.0052 | 0.0043 | 0.495 |
| kidslt6 | 0.1279 | 0.1331 | 0.1556 | 0.337 |
| kidsge6 | 0.0278 | 0.0420 | 0.0332 | 0.509 |
WLS regression
| parameters | cov | HC3 | p_values | |
|---|---|---|---|---|
| const | 1.6668 | 0.9508 | 0.8122 | 0.080 |
| city | -0.0297 | 0.3249 | 0.3553 | 0.927 |
| educ | 0.0275 | 0.0702 | 0.0505 | 0.696 |
| exper | -0.0304 | 0.0198 | 0.0193 | 0.126 |
| nwifeinc | -0.0067 | 0.0156 | 0.0109 | 0.667 |
| kidslt6 | 0.0141 | 0.4841 | 0.4108 | 0.977 |
| kidsge6 | -0.0394 | 0.1435 | 0.1309 | 0.784 |
- La faible hétéroscédasaticité du modèle à été corrigée par l’application de la régression WLS. Les covariances des estimateurs ont baissées et la p-valeur de la statistique de Fisher pour le test d’hétéroscédasticité à augmenté significativement rendant l’hypothèse d’homoscédasticité du modèle WLS plus probable.
Tester le changement de structure de la question 8 entre les femmes qui ont plus de 43 ans et les autres : test sur l’ensemble des coefficients
- Nous allons ici appliquer le test de Chow pour le changement de struture proposé.
Nous souhaitons tester l’égalité des coefficient de la régression:
\[log(wage) = \beta_0 + \beta_{city} city + {\bf \beta_{educ}} educ + \beta_{exper} exper + {\bf \beta_{nwifeinc}} nwifeinc + \beta_{kedslt} kedslt + \beta_{kedsgt} kedsgt\]pour les individus appartenant au groupe $age \leq 43$ et $age > 43$.
En notant respectivement $SSE_c$, $SSE_1$, $SSE_2$ les régressions pour l’ensemble des individus, le groupe $age \leq 43$ et le groupe $age > 43$, le test de student effectué est:
\[f_{stat} = \frac{\frac{(SSE_c - (SSE_1 + SSE_2)}{7}} {\frac{(SSE_1 + SSE_2)}{n - 14}}\]- Regression pour tous les individus
X = sm.add_constant(mroz[["city", "educ", "exper", "nwifeinc", "kidslt6", "kidsge6"]])
y = mroz['lwage']
n, p = X.shape
model = sm.OLS(y, X)
results = model.fit()
SSE_c = np.sum(results.resid**2)
- Regression pour le groupe $age \leq 43$
X = sm.add_constant(mroz.loc[mroz.age <= 43, ["city", "educ", "exper", "nwifeinc", "kidslt6", "kidsge6"]])
y = mroz.loc[mroz.age <= 43, 'lwage']
model = sm.OLS(y, X, hasconst=True)
results = model.fit()
SSE1 = np.sum(results.resid**2)
- Regression pour le groupe $age > 43$
X = sm.add_constant(mroz.loc[mroz.age > 43, ["city", "educ", "exper", "nwifeinc", "kidslt6", "kidsge6"]])
y = mroz.loc[mroz.age > 43, 'lwage']
model = sm.OLS(y, X, hasconst=True)
results = model.fit()
SSE2 = np.sum(results.resid**2)
- Calcul de la statistique
f_stat = ((SSE_c-(SSE1+SSE2)) / p) / ((SSE1+SSE2)/(n-2*p))
p_value = f.sf(f_stat, p, n-2*p)
display_html(pd.DataFrame({"f-stat": f_stat, "p-value": p_value}, index=["results"])\
.style.format({'f-stat': "{:.3f}", 'p-value': "{:.3f}"}))
| f-stat | p-value | |
|---|---|---|
| results | 0.826 | 0.566 |
- La p-valeur du test de Chow est 0.566, on en peut donc pas rejéter l’hypothèse nulle. Il n’y a donc pas de changement de structure entre les deux groupes d’individus considérés.
Ajouter au modèle de la question 7 la variable huseduc. Faire ensuite la même régression en décomposant la variable huseduc en 4 variables binaires construites selon votre choix
| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| huseduc | 428.0 | 12.61215 | 3.035163 | 4.0 | 11.0 | 12.0 | 16.0 | 17.0 |
- Nous allons décomposer la variable
huseducen 4 variables binaires correspondant à l’appartenance aux fractiles $\bf\frac{1}{4}, \bf\frac{1}{2}, \bf\frac{3}{4}$ et 1.
fractiles = [mroz["huseduc"].quantile(q) for q in [0, 0.25, 0.5, 0.75, 1]]
masks = np.empty((mroz.shape[0], 3))
for i in range(len(fractiles)-2):
masks[:, i] = (mroz["huseduc"]>=fractiles[i]) & (mroz["huseduc"]<fractiles[i+1])
huseduc_decomp = pd.DataFrame(data=masks, columns=["huseduc_0_25", "huseduc_25_50", "huseduc_50_75"])
X = sm.add_constant(pd.concat([mroz[["city", "educ", "exper", "nwifeinc", "kidslt6", "kidsge6"]], huseduc_decomp], axis=1))
y = mroz["lwage"]
model = sm.OLS(y, X)
results = model.fit()
residual = results.resid
display_html(OLS_summary(results))
| parameters | cov | HC3 | p_values | |
|---|---|---|---|---|
| const | -0.7216 | 0.2798 | 0.2520 | 0.010 |
| city | 0.0437 | 0.0704 | 0.0686 | 0.534 |
| educ | 0.1165 | 0.0176 | 0.0161 | 0.000 |
| exper | 0.0149 | 0.0045 | 0.0045 | 0.001 |
| nwifeinc | 0.0061 | 0.0034 | 0.0031 | 0.073 |
| kidslt6 | -0.0309 | 0.0857 | 0.1071 | 0.718 |
| kidsge6 | -0.0141 | 0.0270 | 0.0287 | 0.601 |
| huseduc_0_25 | 0.1672 | 0.1146 | 0.1099 | 0.145 |
| huseduc_25_50 | 0.1788 | 0.1793 | 0.1690 | 0.319 |
| huseduc_50_75 | 0.1617 | 0.0897 | 0.0902 | 0.072 |
- Test de non significativité de l’ensemble des variables binaires:
X = sm.add_constant(pd.concat([mroz[["city", "educ", "exper", "nwifeinc", "kidslt6", "kidsge6"]], huseduc_decomp], axis=1))
y = mroz["lwage"]
model = sm.OLS(y, X)
results = model.fit()
residual = results.resid
SSE = np.sum(residual**2)
X = sm.add_constant(mroz[["city", "educ", "exper", "nwifeinc", "kidslt6", "kidsge6"]])
y = mroz["lwage"]
model = sm.OLS(y, X)
results = model.fit()
residual = results.resid
SSE1 = np.sum(residual**2)
# --- Compute Fisher Stat --- #
f_stat = ((SSE1 - SSE) / 3) / (SSE / (n - p))
p_value = f.sf(f_stat, 3, n - p)
display_html(pd.DataFrame({"f-stat": f_stat, "p-value": p_value}, index=["results"])\
.style.format({'f-stat': "{:.3f}", 'p-value': "{:.3f}"}))
| f-stat | p-value | |
|---|---|---|
| results | 1.143 | 0.331 |
- La p-valeur du test est 0.331, ainsi, les variable binaires associées à la varibale huseduc ne sont pas significatives dans l’ensemble.
